Question

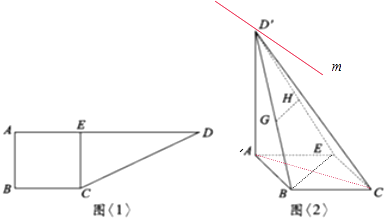
【题目】如图＜1＞：在直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=BC=2，AD=6，CE⊥AD于E点，把△DEC沿CE折到D′EC的位置，使D′A=2 ，如图＜2＞：若G，H分别为D′B，D′E的中点．
（1）求证：GH⊥平面AD′C；
（2）求平面D′AB与平面D′CE的夹角．

Answer 1

【答案】
（1）证明：∵在直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=BC=2，AD=6，CE⊥AD于E点，

把△DEC沿CE折到D′EC的位置，使D′A=2 ，

∴AE=CE=2，D′E=6﹣2=4，∴D′A2+AE2=D′E2，CD′= =2 ，

∴AD′⊥AE，∵AD′⊥AB，AD′∩AB=A，∴AD′⊥平面ABCE，∴面AD′C⊥ABCE，又因为ABCE是正方形，∴BE⊥AC，

BE⊥面ACD′，∵G，H分别为D′B，D′E的中点，∴GH∥BE，∴GH⊥平面AD′C

（2）解：如图过点D′作直线m∥AB，∵AB∥EC，∴直线m就是面D′AB与平面D′CE的交线，

∵CE⊥AE，面AED′⊥面ABCE于AE，∴CE⊥D′E，即D′E⊥m，

∵AD′⊥AB，∴AD′⊥m，∵AD′面AD′B，D′ED′CE，∴∠AD′E就是平面D′AB与平面D′CE的夹角的平面角，

在直角三角形AD′E中，AE=2，D′E=4，可得，∴∠AD′E=30°．

平面D′AB与平面D′CE的夹角为300

【解析】（1）证明BE⊥面ACD′，GH∥BE，即可得到GH⊥平面AD′C．（2）如图过点D′作直线m∥AB，由AB∥EC，得直线m就是面D′AB与平面D′CE的交线，可得∠AD′E就是平面D′AB与平面D′CE的夹角的平面角，
【考点精析】利用直线与平面垂直的判定对题目进行判断即可得到答案，需要熟知一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．