【题目】设等比数列
的前n项和为Sn，已知a1=2，且4S1，3S2，2S3成等差数列．
（Ⅰ）求数列的通项公式；
（Ⅱ）设
，求数列{bn}的前n项和Tn．
【答案】（Ⅰ）
（Ⅱ）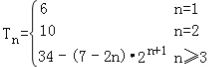
【解析】
试题分析：（Ⅰ）根据4S1，3S2，2S3成等差数列．根据等差中项6S2=4S1+2S3，化简整理求得q=2，写出通项公式；（Ⅱ）讨论当n=1、2时，求得T1=6，T2=10，写出前n项和，采用错位相减法求得Tn
试题解析：（Ⅰ）∵4S1，3S2，2S3成等差数列，
∴6S2=4S1+2S3， 即6（a1+a2）=4a1+2（a1+a2+a3），
则：a3=2a2，q=2， ∴
；.................................5分
（Ⅱ）当n=1，2时，T1=6，T2=10，
当n≥3，Tn=10+1×23+3×24+…+（2n﹣5）2n，
2Tn=20+1×24+3×25+…+（2n﹣7）×2n+（2n﹣5）×2n+1，
两式相减得：﹣Tn=﹣10+8+2（24+25+…+2n）﹣（2n﹣5）×2n+1，..........9分
=﹣2+2×
﹣（2n﹣5）×2n+1，
=﹣34+（7﹣2n）2n+1，
∴Tn=34﹣（7﹣2n）2n+1．
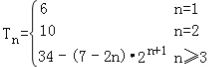∴．..........12分
举一反三同步巧讲精练系列答案科目：高中数学 来源： 题型：
【题目】已知函数
的图象上有一点列
，点
在
轴上的射影是
，且
(
且
)， 
.
(1)求证： 
是等比数列，并求出数列
的通项公式；
(2)对任意的正整数
，当
时，不等式
恒成立，求实数
的取值范围.
(3)设四边形
的面积是
，求证： 
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学有学生 
人，其中一年级 
人，二、三年级各 
人，现要用抽样方法抽取 
人形成样本，将学生按一、二、三年级依次统一编号为 
， 
， 
， 
，如果抽得号码有下列四种情况：
①
， 
， 
， 
， 
， 
， 
， 
， 
， 
；
②
， 
， 
， 
， 
， 
， 
， 
， 
， 
；
③
， 
， 
， 
， 
， 
， 
， 
， 
， 
；
④
， 
， 
， 
， 
， 
， 
， 
， 
， 
；
其中可能是由分层抽样得到，而不可能是由系统抽样得到的一组号码为 
A. ①② B. ②③ C. ①③ D. ①④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】根据下列算法语句，将输出的A值依次记为a1，a2，…，an，…，a2015；已知函数f（x）=a2sin（ωx+φ）（ω＞0，|φ|＜
）的最小正周期是a1，且函数
的图象关于直线x=
对称。
（Ⅰ）求函数表达式；
（Ⅱ）已知△ABC中三边a,b,c对应角A,B,C，a＝4，b＝4
，∠A＝30°，求
。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地区有小学21所，中学14所，大学7所，现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查．
（1）求应从小学、中学、大学中分别抽取的学校数目；
（2）若从抽取的6所学校中随机抽取2所学校做进一步数据分析，
①列出所有可能的抽取结果；
②求抽取的2所学校均为小学的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
