
【题目】如图, 四棱锥![]() 中, 平面
中, 平面![]() 平面
平面![]() ,
,![]() 为线段
为线段![]() 上一点,
上一点,![]() 为
为![]() 的中点.
的中点.
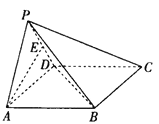
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接![]() ,设
,设![]() ,可证四边形
,可证四边形![]() 为平行四边形,得
为平行四边形,得![]() 是
是![]() 的中点,利用三角形中位线定理可得
的中点,利用三角形中位线定理可得![]() 进而由线面平行的判定定理可得结论;(2)先证
进而由线面平行的判定定理可得结论;(2)先证![]() 平面
平面![]() ,分别以
,分别以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 为
为![]() 轴正方向,空间直角坐标系
轴正方向,空间直角坐标系![]() ,分别求出平面
,分别求出平面![]() 和平面
和平面![]() 的法向量,利用空间向量夹角余弦公式可得二面角
的法向量,利用空间向量夹角余弦公式可得二面角![]() 的余弦值,进而得结果.
的余弦值,进而得结果.
试题解析:(1)证明: 连接![]() ,设
,设![]() ,连接
,连接![]() ,
,![]() 四边形
四边形![]() 为平行四边形, 且
为平行四边形, 且![]() 是
是![]() 的中点, 又
的中点, 又![]() 为
为![]() 的中点,
的中点,![]() 平面
平面![]() 平面
平面![]() 平面
平面![]() .
.
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,由
,由![]() 得
得![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() 平面
平面![]() ,在
,在![]() 中,
中,![]() , 在等腰
, 在等腰![]() 中,
中,![]() , 以
, 以![]() 为坐标原点, 分别以
为坐标原点, 分别以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 为
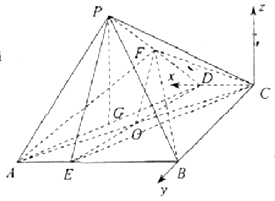
为![]() 轴正方向, 建立如图所示的空间直角坐标系
轴正方向, 建立如图所示的空间直角坐标系![]() ,由题知,
,由题知,![]()
设![]() 是平面
是平面![]() 的法向量, 则
的法向量, 则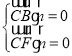 ,即
,即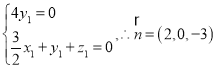 .
.
设![]() 是平面
是平面![]() 的法向量, 则
的法向量, 则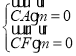 ,即
,即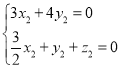 得
得![]() .
.
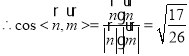 ,
,![]() 二面角
二面角![]() 的正弦值为
的正弦值为![]() .
.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,正四面体![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 分别在两两垂直的三条射线
分别在两两垂直的三条射线![]() ,
, ![]() ,
, ![]() 上,则在下列命题中,错误的是( )
上,则在下列命题中,错误的是( )
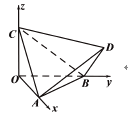
A. ![]() 是正三棱锥
是正三棱锥
B. 直线![]() 与平面
与平面![]() 相交
相交
C. 直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]()
D. 异面直线![]() 和
和![]() 所成角是
所成角是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等比数列![]() 的前n项和为Sn,已知a1=2,且4S1,3S2,2S3成等差数列.
的前n项和为Sn,已知a1=2,且4S1,3S2,2S3成等差数列.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】迭代法是用于求方程或方程组近似根的一种常用的算法设计方法.设方程为![]() ,用某种数学方法到处等价的形式
,用某种数学方法到处等价的形式![]() ,然后按以下步骤执行:
,然后按以下步骤执行:
(1)选一个方程的近似根,赋给变量![]() ;
;
(2)将![]() 的值保存于变量
的值保存于变量![]() ,然后计算
,然后计算![]() ,并将结果存于变量
,并将结果存于变量![]() ;
;
(3)当![]() 与
与![]() 的差的绝对值还小于指定的精度要求时,重复步骤(2)的计算.若方程有根,则按上述方法求得的
的差的绝对值还小于指定的精度要求时,重复步骤(2)的计算.若方程有根,则按上述方法求得的![]() 就认为是方程的根.试用迭代法求某个数的平方根,用流程图和伪代码表示问题的算法.
就认为是方程的根.试用迭代法求某个数的平方根,用流程图和伪代码表示问题的算法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有工人1000名,其中250名工人参加短期培训(称为![]() 类工人),另外750名工人参加过长期培训(称为
类工人),另外750名工人参加过长期培训(称为![]() 类工人).现用分层抽样方法(按
类工人).现用分层抽样方法(按![]() 类,
类,![]() 类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(1)![]() 类工人和
类工人和![]() 类工人中个抽查多少工人?
类工人中个抽查多少工人?
(2)从![]() 类工人中的抽查结果和从
类工人中的抽查结果和从![]() 类工人中的抽查结果分别如下表1和表2.
类工人中的抽查结果分别如下表1和表2.
表1:

表2:

① 先确定![]() ,
,![]() ,再完成下列频率分布直方图,就生产能力而言,
,再完成下列频率分布直方图,就生产能力而言,![]() 类工人中个体间的差异程度与
类工人中个体间的差异程度与![]() 类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
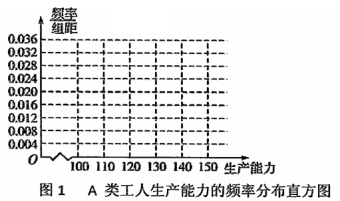
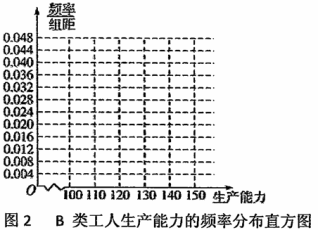
② 分别估计![]() 类工人和
类工人和![]() 类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中
类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中
的数据用该组区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是二次函数,不等式
是二次函数,不等式![]() 的解集是
的解集是![]() ,且
,且![]() 在区间
在区间![]() 上的最大值是12.
上的最大值是12.
(1)求![]() 的解析式;
的解析式;
(2)是否存在自然数![]() ,使得方程
,使得方程![]() 在区间
在区间![]() 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要付出设备的维修和工人工资等费用![]() 的信息如下图.
的信息如下图.

(1)求![]() ;
;
(2)引进这种设备后,第几年后该公司开始获利;
(3)这种设备使用多少年,该公司的年平均获利最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com