
分析 由焦点在y轴上,设出双曲线方程,求出渐近线方程,得到2a=3b,再由a,b,c的关系及离心率公式,计算即可得到.
解答 解:∵双曲线的焦点在y轴上,
∴设双曲线的方程为$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)
可得双曲线的渐近线方程是y=±$\frac{a}{b}$x,
结合题意双曲线的渐近线方程是y=±$\frac{3}{2}$x,得$\frac{a}{b}$=$\frac{3}{2}$,
∴b=$\frac{2}{3}$a,可得c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{{a}^{2}+\frac{4}{9}{a}^{2}}$=$\frac{\sqrt{13}}{3}$a,
因此,此双曲线的离心率e=$\frac{c}{a}$=$\frac{\sqrt{13}}{3}$
故答案为:$\frac{\sqrt{13}}{3}$.
点评 本题考查双曲线的方程和性质,主要考查渐近线方程和离心率的求法,利用待定系数法是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
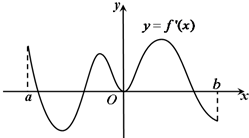 函数f(x)的导函数f′(x)在区间(a,b)内的图象如图所示,则f(x)在(a,b)内的极大值点有( )
函数f(x)的导函数f′(x)在区间(a,b)内的图象如图所示,则f(x)在(a,b)内的极大值点有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 棱台的侧面一定不会是平行四边形 | |
| B. | 棱锥的侧面只能是三角形 | |
| C. | 由四个面围成的封闭图形只能是三棱锥 | |
| D. | 棱锥被平面截成的两部分不可能都是棱锥 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {4} | C. | {2,4} | D. | {2,4,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com