练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知椭圆
    x2
    5
    +y2=1，椭圆的中心为坐标原点O，点F是椭圆的右焦点，点A是椭圆短轴的一个端点，过点F的直线l与椭圆交于M、N两点，与OA所在直线交于E点，若
    EM
    =λ1
    MF
    ，
    EN
    =λ2
    NF
    ，则λ1+λ2=（　　）
    A、-10B、10C、-5D、5
    考点：直线与圆锥曲线的关系
    专题：综合题,圆锥曲线的定义、性质与方程
    分析：设M（x1，y1），N（x2，y2）（x1＞x2）则由
    EM
    =λ1
    MF
    ，
    EN
    =λ2
    NF
    ，可得λ1+λ2=
    x2
    2-x2
    +
    x1
    2-x1
    ，设直线方程为y=k（x-2），代入椭圆方程，利用韦达定理，即可得出结论．
    解答： 解：设M（x1，y1），N（x2，y2）（x1＞x2）则
    ∵椭圆
    x2
    5
    +y2=1，∴c=2，
    ∵
    EM
    =λ1
    MF
    ，
    EN
    =λ2
    NF
    ，∴λ1+λ2=
    x2
    2-x2
    +
    x1
    2-x1

    设直线方程为y=k（x-2），代入椭圆方程可得（1+5k2）x-20k2x+20k2-5=0，
    ∴x1+x2=
    20k2
    1+5k2
    ，x1x2=
    20k2-5
    1+5k2
    ，
    ∴
    x2
    2-x2
    +
    x1
    2-x1
    =
    2(x1+x2)-2x1x2
    4-2(x1+x2)+x1x2
    =-10，
    ∴λ1+λ2=-10．
    故选：A．
    点评：本题考查向量知识的运用，考查直线与椭圆的位置关系，考查学生分析解决问题的能力，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    对于数列{an}，a1=4，an+1=f（an），n=1，2…，其中f（x）如表所示
    x 1 2 3 4 5
    f（x） 5 4 3 1 2
    则a2014等于（　　）
    A、1B、2C、3D、5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在一次运动会上有四项比赛的冠军在甲、乙、丙三人中产生，那么不同的夺冠情况共有（　　）种．
    A、A
     
    3
    4
    B、43
    C、34
    D、C
     
    3
    4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等比数列{an}中，a5=3，则a1•a2•a3…a9=39，若数列{bn}为等差数列，b5=3，则数列{bn}的类似结论为（　　）
    A、b1b2…b9=39
    B、b1+b2+…+b9=39
    C、b1b2…b9=3×9
    D、b1+b2+…+b9=3×9

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    掌握数学，一个美好的祝愿：张开你的右手，你将看到你的掌纹，有人称它是命运的密语，其实是我们所熟悉函数的图象，每天都握在我们的掌心．某人的掌纹如图所示，在所给的直角坐标系中，它们只可能是下列给出的5个函数中的（　　）
    ①y=（
    3
    2
    ）x  
    ②y=（
    2
    3
    ）x   
    ③y=
    		x
    -
    1
    2
      
    ④y=ln（x+
    1
    2
    ）   
    ⑤y=ln（x-
    1
    2
    ）
    A、②③⑤B、①③④
    C、①③⑤D、②③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

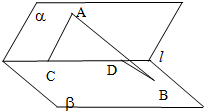    如图，已知二面角α-l-β为60°，点A∈α，AC⊥l，C为垂足，点B∈β，BD⊥l，D为垂足，且AC=2，CD=3，DB=1，则AB的长度为（　　）
    A、4
    B、2
    		3
    C、3
    		3
    D、
    3
    2
    		6

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    cos（-60°）=（　　）
    A、
    1
    2
    B、
    		3
    2
    C、-
    1
    2
    D、-
    		3
    2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知公差大于零的等差数列{an}的前n项和为Sn，且满足：a3•a4=117，a2+a5=22．
    （1）求数列{an}的通项公式an；
    （2）若数列{bn}是等差数列，且bn=
    Sn
    n+c
    ，求非零常数c；
    （3）在（2）的条件下，设cn=an2-λbn，已知数列{cn}为递增数列，求实数λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f（x）是定义在R上的单调函数，对任意的实数m，n总有：f（m+n）=f（m）•f（n）且x＞0时，0＜f（x）＜1．
    （1）证明：f（0）=1且x＜0时f（x）＞1；
    （2）当f（4）=
    1
    16
    ，求使f（x2-1）•f（a-2x）≤
    1
    4
    对任意实数x恒成立的参数a的取值范围．

    查看答案和解析>>

    同步练习册答案