已知函数f(x)=x3+(a-1)x2+3x+b的图象与x轴有三个不同交点,且交点的横坐标分别可作为抛物线、双曲线、椭圆的离心率,则实数a的取值范围是________.
(-3,-2)
分析:先把函数f(x)=x
3+(a-1)x
2+3x+b的图象与x轴有三个不同交点转化为方程x
3+(a-1)x
2+3x+b=0有三个不等实根.再根据1是方程的根代入求出b和a之间的关系式;代入原方程分解因式,最后转化为x
2+a(x+1)+3=0有两个根,且一个根在(0,1)上,另一根在(1,+∞)上,再借助于图象求出实数a的取值范围即可.
解答:
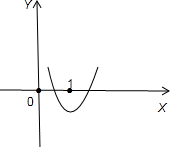
解:函数f(x)=x
3+(a-1)x
2+3x+b的图象与x轴有三个不同交点,即是方程x
3+(a-1)x
2+3x+b=0有三个不等实根.
由题得1是方程的根,故有1+(a-1)+3+b=0?b=-a-3?x
3+(a-1)x
2+3x+b=x
3+(a-1)x
2+3x-a-3=(x-1)[x
2+a(x+1)+3]=0.
因为交点的横坐标分别可作为抛物线、双曲线、椭圆的离心率
故方程g(x)=x
2+a(x+1)+3=0有两个根,且一个根在(0,1)上,另一根在(1,+∞)上,
由图得,
有g(0)>0且g(1)<0?a>-3且a<-2,
故满足要求的实数a的取值范围是(-3,-2).
故答案为:(-3,-2).
点评:本题主要考查根的个数问题以及一元二次根的分布问题.在解决一元二次方程根的分布问题时,常常是把其对应函数的图象找出来,借助于图象来解.

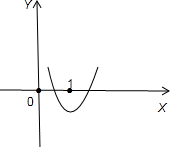 解:函数f(x)=x3+(a-1)x2+3x+b的图象与x轴有三个不同交点,即是方程x3+(a-1)x2+3x+b=0有三个不等实根.
解:函数f(x)=x3+(a-1)x2+3x+b的图象与x轴有三个不同交点,即是方程x3+(a-1)x2+3x+b=0有三个不等实根.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<