
【题目】在![]() 中,
中,![]() ,斜边
,斜边![]() .
.![]() 可以通过
可以通过![]() 以直线
以直线![]() 为轴旋转得到,且二面角
为轴旋转得到,且二面角![]() 是直二面角.动点
是直二面角.动点![]() 的斜边
的斜边![]() 上.
上.
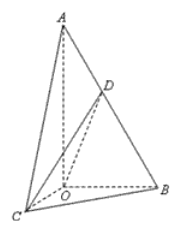
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦的最大值.
所成角的正弦的最大值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)由题意得出平面![]() 平面
平面![]() ,由旋转的性质得出
,由旋转的性质得出![]() ,由平面与平面垂直的性质定理得出
,由平面与平面垂直的性质定理得出![]() 平面
平面![]() ,再利用平面与平面垂直的判定定理得出平面
,再利用平面与平面垂直的判定定理得出平面![]() 平面
平面![]() ;
;
(2)计算出![]() ,由(1)可知,
,由(1)可知,![]() 平面
平面![]() ,于是得出直线
,于是得出直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,可得出
,可得出![]() ,得知当
,得知当![]() 时,
时,![]() 最小,由此可求出直线
最小,由此可求出直线![]() 与平面
与平面![]() 所成角的正弦的最大值.
所成角的正弦的最大值.
(1)![]() 为直角三角形,且斜边为
为直角三角形,且斜边为![]() ,
,![]() .
.
将![]() 以直线
以直线![]() 为轴旋转得到
为轴旋转得到![]() ,则
,则![]() ,即
,即![]() .
.
![]() 二面角
二面角![]() 是直二面角,即平面
是直二面角,即平面![]() 平面
平面![]() .
.
又平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,因此,平面
,因此,平面![]() 平面
平面![]() ;
;
(2)在![]() 中,
中,![]() ,斜边
,斜边![]() ,
,![]() 且
且![]() .
.
由(1)知,![]() 平面
平面![]() ,所以,直线
,所以,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
当![]() 时,
时,![]() 取最小值,此时
取最小值,此时![]() 取最大值,且
取最大值,且![]() .
.
因此,![]() ,
,
即直线![]() 与平面
与平面![]() 所成角的正弦的最大值为
所成角的正弦的最大值为![]() .
.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且acosC+ccosA=2bcosA.
(1)求角A的值;
(2)若![]() ,
, ![]() ,求△ABC的面积S.
,求△ABC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产![]() 、
、![]() 两种产品,生产每
两种产品,生产每![]() 产品所需的劳动力和煤、电消耗如下表:
产品所需的劳动力和煤、电消耗如下表:
产品品种 | 劳动力(个) | 煤 | 电 |
|
|
|
|
|
|
|
|
已知生产![]() 产品的利润是
产品的利润是![]() 万元,生产
万元,生产![]() 产品的利润是
产品的利润是![]() 万元.现因条件限制,企业仅有劳动力
万元.现因条件限制,企业仅有劳动力![]() 个,煤
个,煤![]() ,并且供电局只能供电
,并且供电局只能供电![]() ,则企业生产
,则企业生产![]() 、
、![]() 两种产品各多少吨,才能获得最大利润?
两种产品各多少吨,才能获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是我省某地区2012年至2018年农村居民家庭年纯收入![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
年纯收入 | 2 | 3 | 3.5 | 4 | 4.5 | 5 | 6 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2012年至2018年该地区农村居民家庭年纯收入的变化情况,并预测该地区2019年农村居民家庭年纯收入(结果精确到0.1)。
附:回归直线的斜率和截距的最小二乘法估计公式分别为: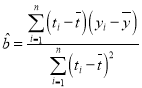 ,
,![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有9只球,其中标有数字1,2,3,4的小球各2个,标数字5的小球有1个.从袋中任取3个小球,每个小球被取出的可能性都相等,用![]() 表示取出的3个小球上的最大数字.
表示取出的3个小球上的最大数字.
(1)求取出的3个小球上的数字互不相同的概率;
(2)求随机变量![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com