
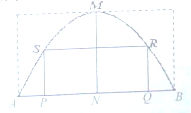
 如图是一块外轮廓线(A,B间的曲线部分)为抛物线的钢板,MN为抛物线的对称轴,A,B是抛物线上关于MN对称的两点,其中AB=2,MN=1,先要将其割成矩形PQRS,使矩形的两个顶点P,Q落在线段AB上,另两个顶点R,S落在抛物线上.(1)建立适当的直角坐标系,求出这一抛物线的方程;
如图是一块外轮廓线(A,B间的曲线部分)为抛物线的钢板,MN为抛物线的对称轴,A,B是抛物线上关于MN对称的两点,其中AB=2,MN=1,先要将其割成矩形PQRS,使矩形的两个顶点P,Q落在线段AB上,另两个顶点R,S落在抛物线上.(1)建立适当的直角坐标系,求出这一抛物线的方程; 解:(1)如图,以顶点M为原点,抛物线的对称轴为y轴,
解:(1)如图,以顶点M为原点,抛物线的对称轴为y轴,| 1 |
| 2 |
| ||
| 3 |
| x | (0,
|
| (
| ||||||||||||
| S′(x) | + | 0 | - | ||||||||||||
| S(x) | 上升 |
| 下降 |
| ||
| 3 |
| 4 |
| 9 |
| 3 |
| 4 |
| 9 |
| 3 |


科目:高中数学 来源: 题型:
| 销售单价x(元) | 35 | 40 | 45 | 50 |
| 日销售量y(件) | 56 | 41 | 28 | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 数列{an}满足an+1=
数列{an}满足an+1=| 1 |
| 2-an |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
A、
| ||||
| B、6 | ||||
| C、12 | ||||
D、7
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、l⊥g,且l与圆相离 |
| B、l⊥g,且l与圆相切 |
| C、l∥g,且l与圆相交 |
| D、l∥g,且l与圆相离 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com