练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．下列向量中，可以作为基底的是（　　）
    A．$\overrightarrow{{e}_{1}}$=（0，0），$\overrightarrow{{e}_{2}}$=（1，-2）B．$\overrightarrow{{e}_{1}}$=（2，-3），$\overrightarrow{{e}_{2}}$=（-$\frac{1}{2}$，$\frac{3}{4}$）
    C．$\overrightarrow{{e}_{1}}$=（3，5），$\overrightarrow{{e}_{2}}$=（6，10）D．$\overrightarrow{{e}_{1}}$=（1，-2），$\overrightarrow{{e}_{2}}$=（5，7）

    分析 平面内任意两个不共线的向量都可以作为基底，判断各个徐昂项中的两个向量是否共线，从而得出结论．

    解答 解：平面内任意两个不共线的向量都可以作为基底，由于向量（1，2）和向量（5，7）不共线，
    故可以作为基底，
    而其它选项中的2个向量的坐标对应成比例，故其它选项中的2个向量是共线向量，不能作为基底，
    故选：D．

    点评 题主要考查基地的定义，两个向量是否共线的判定方法，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    1．已知定义在R上的函数f（x）满足f（1）=1，且对于任意的x，f′（x）$＜\frac{1}{2}$恒成立，则不等式f（lg2x）＜$\frac{l{g}^{2}x}{2}$+$\frac{1}{2}$的解集为（　　）
    A．（0，$\frac{1}{10}$）B．（10，+∞）C．（$\frac{1}{10}$，10）D．（0，$\frac{1}{10}$）∪（10，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．某几何体的三视图如图所示，按图中所给的尺寸，该几何体的体积为（　　）
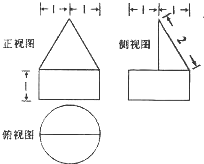
    A．$\frac{\sqrt{3}π}{6}$+1B．$\frac{\sqrt{3}π}{6}$+πC．$\frac{\sqrt{3}π}{3}$+πD．$\frac{\sqrt{3}π}{3}$+1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．正方形ABCD与正方形ABEF互相垂直，点M，N，G分别是AE，BC，CE的中点，AB=2，
    （1）求证：BE⊥MG
    （2）求证：MN∥平面EFDC
    （3）求多面体A-EFDC的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．定义在（0，+∞）的函数f（x）为单调函数，对任意的x∈（0，+∞）恒有f[f（x）-log4x]=5．x0是方程f（x）-f′（x）=4的一个根，则x0所在区间为（　　）
    A．（1，2）B．（2，3）C．（3，4）D．（4，5）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．求值：tan40°+tan20°+$\sqrt{3}$tan40°•tan20°=$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．在空间中，设直线l的方向向量为$\overrightarrow{a}$，平面α的法向量为$\overrightarrow{b}$，对于原命题“若$\overrightarrow{a}$•$\overrightarrow{b}$=0，则l∥α”，下列判断正确的是（　　）
    A．原命题为真，否命题为真B．原命题为假，否命题为假
    C．原命题为假，否命题为真D．原命题为真，否命题为假

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

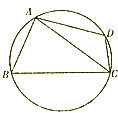    20．某棚户区改造工程规划用地近似为图中半径为R的圆面，图中圆内接四边形ABCD为拟定拆迁的棚户区，测得AB=AD=4百米，BC=6百米，CD=2百米．
    （1）请计算原棚户区ABCD的面积及圆面的半径R；
    （2）因地理条件的限制，边界AD，CD不能变更，而边界AB、BC可以调整，为了提高棚户区改造建设用地的利用率，请在圆弧ABC上求出一点P，使得棚户区改造的新建筑用地APCD的面积最大，并求最大值．（注：圆的内接四边形对角互补）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．过顶点在原点，焦点在y轴正半轴的抛物线的焦点F作直线l交抛物线于A、B两点，过点A、B分别作抛物线准线的垂线，垂足分别为点C、D，|AF|=2|BF|，且$\overrightarrow{DC}$•$\overrightarrow{BA}$=72，则该抛物线方程为（　　）
    A．x2=8yB．x2=10yC．x2=9yD．x2=5y

    查看答案和解析>>

    同步练习册答案