
分析 (1)设出直线方程,利用直线与圆的位置关系,列出不等式求解即可.
(2)设出M,N的坐标,利用直线与圆的方程联立,通过韦达定理,结合已知条件,转化为向量的数量积,求出直线的斜率,然后判断直线与圆的位置关系求解|MN|即可.
解答 解:(1)由题设,可知直线l的方程为y=kx+1,因为直线l与圆C交于两点,
所以$\frac{|2k-3+1|}{\sqrt{1+{k}^{2}}}$<1.解得$\frac{4-\sqrt{7}}{3}$<k<$\frac{4+\sqrt{7}}{3}$.
所以k的取值范围为:($\frac{4-\sqrt{7}}{3}$,$\frac{4+\sqrt{7}}{3}$).
(2)设M(x1,y1),N(x2,y2).将y=kx+1代入方程:(x-2)2+(y-3)2=1,
整理得(1+k2)x2-4(1+k)x+7=0.所以x1+x2=$\frac{4(1+k)}{1+{k}^{2}}$,x1x2=$\frac{7}{1+{k}^{2}}$,
$\overrightarrow{OM}•\overrightarrow{ON}$=x1x2+y1y2=(1+k)2(x1x2)+k(x1+x2)+1=$\frac{4k(1+k)}{1+{k}^{2}}+8$.
由题设可得S△MON=6tan∠MON,可得$\overrightarrow{OM}•\overrightarrow{ON}$=12.
即$\frac{4k(1+k)}{1+{k}^{2}}+8$=12,解得k=1,所以直线l的方程为y=x+1.
故圆心C在直线l上,所以|MN|=2.
点评 本题考查直线与圆的位置关系的综合应用,圆的方程的应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(岁) | 频率 | |
| 第1组 | [25,30) | 0.1 |
| 第2组 | [30,35) | 0.1 |
| 第3组 | [35,40) | 0.4 |
| 第4组 | [40,45) | 0.3 |
| 第5组 | [45,50] | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
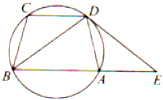 如图,已知圆上的四点A、B、C、D,CD∥AB,过点D的圆的切线DE与BA的延长线交于E点.
如图,已知圆上的四点A、B、C、D,CD∥AB,过点D的圆的切线DE与BA的延长线交于E点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | 2017 | C. | 1007 | D. | 1008 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com