
(本题满分12分)班主任为了对本班学生的考试成绩进行分析,决定从全班 位女同学,
位女同学, 位男同学中随机抽取一个容量为
位男同学中随机抽取一个容量为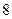 的样本进行分析。
的样本进行分析。
(Ⅰ)如果按性别比例分层抽样,可以得到多少个不同的样本(只要求写出算式即可,不必计算出结果);
(Ⅱ)随机抽取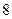 位同学,数学成绩由低到高依次为:
位同学,数学成绩由低到高依次为: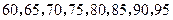 ;
;
物理成绩由低到高依次为: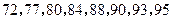 ,若规定
,若规定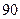 分(含
分(含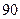 分)以
分)以 上为优秀,记
上为优秀,记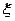 为这
为这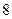 位同学中数学和物理分数均为优秀的人数,求
位同学中数学和物理分数均为优秀的人数,求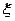 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)若这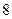 位同学的数学、物理分数事实上对应下表:
位同学的数学、物理分数事实上对应下表:
| 学生编号 | 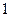 | 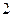 | 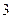 | 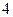 | 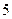 | 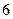 | 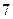 | 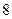 |
数学分数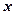 | 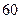 | 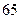 | 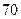 | 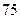 | 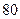 | 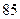 | 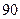 |  |
物理分数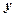 | 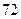 | 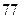 | 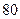 | 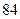 | 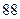 | 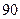 | 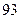 |  |
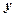 与
与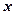
 之间具有较强的线性相关关系,求出
之间具有较强的线性相关关系,求出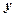 与
与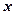 的线性回归方程(系数精确到
的线性回归方程(系数精确到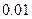 ).(参考公式:
).(参考公式: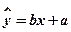 ,其中
,其中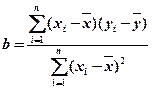 ,
,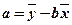 ; 参考数据:
; 参考数据: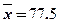 ,
,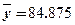 ,
,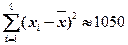 ,
, ,
,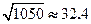 ,
,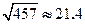 ,
,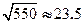 )
)  同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分) 某种产品的广告费用支出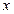 (万元)与销售额y(万元)之间有如下的对应数据
(万元)与销售额y(万元)之间有如下的对应数据
(1)求回归直线方程;
(2)据此估计广告费用为10销售收入 的值
的值
(参考 公式:
公式: 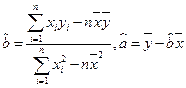 )
)
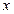 |  2 2 | 4 | 5 | 6 | 8 |
 | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题10分)
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人. 女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(Ⅰ)根据以上数据建立一个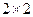 的列联表;
的列联表;
(Ⅱ)判断性别与休闲方式是否有关系.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36.
(1)求样本容量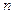 ;
;
(2)求样本中净重大于或等于98克并且小于104克的产品的个数;
(3)求样本产品净重的中位数的估计值.(小数点后保留一位)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某校高三数学竞赛初赛考试后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六 组,第一组
组,第一组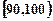 、第二组
、第二组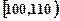 …第六组
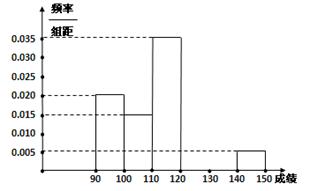
…第六组 . 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
. 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
(Ⅰ)请补充完整频率分布直方图,并估
计这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第四组和第六组
中任意选2人,记他们的成绩分别
为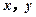 . 若
. 若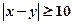 ,则称此二
,则称此二
人为“黄金帮扶组”,试求选出的二
人错误!链接无效。的概率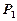 ;
;
(Ⅲ)以此样本的频率当作概率,现随机在这组样本中选出的3名学生,求成绩不低于
120分的人数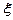 分布列及期望
分布列及期望 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某公司近年来科研费用支出 万元与公司所获得利润
万元与公司所获得利润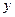 万元之间有如下的统计数据:
万元之间有如下的统计数据:
 | 2 | 3 | 4 | 5 |
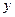 | 18 | 27 | 32 | 35 |
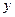 关于
关于 的线性回归方程
的线性回归方程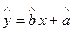 ;
;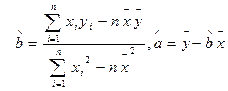
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
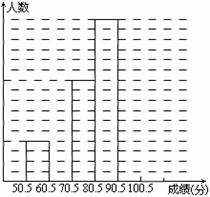
(本题满分14分)为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数条形图,解答下列问题:
(Ⅰ)填充频率分布表的空格(将答案直接填在表格内);
(Ⅱ)补全频数条形图;
(Ⅲ)学校决定成绩在75.5~85.5分的学生为二等奖,问该校获得二等奖的学生约为多少人?
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | | 0.16 |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | | |
| 合计 | 50 | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校组织一次篮球投篮测试,已知甲同学每次投篮的命中率均为1/2。
(1)若规定每投进1球得2分,甲同学投篮4次,求总得分X的概率分布和数学期望。
(2)假设连续3次投篮未中或累计7次投篮未中,则停止投篮测试,问:甲同学恰好投篮10次,被停 止投篮测试的概率是多少?
止投篮测试的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com