
 f(2x)+1?恒成立.令x=
f(2x)+1?恒成立.令x= ,则得f(
,则得f( )≤
)≤ ,连续应用?式,
,连续应用?式,

 ≤…
≤… =
=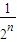 故f(2-n)≤2-n+2(n∈N*);②若x∈(0,1]),则必存在n∈N*,使得∈(
故f(2-n)≤2-n+2(n∈N*);②若x∈(0,1]),则必存在n∈N*,使得∈( ,
, ],由f(x)是增函数,故f(x)≤f(
],由f(x)是增函数,故f(x)≤f( )≤
)≤ +2,又2x+2>2×
+2,又2x+2>2× +2=
+2= +2,故有f(x)<2x+2.
+2,故有f(x)<2x+2.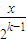 ∈[1,2)
∈[1,2)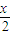 )=4f(
)=4f(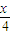 )=…=(-2)k-1f(
)=…=(-2)k-1f(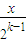 ),
), f(2x)+1恒成立.
f(2x)+1恒成立. ,则得f(
,则得f( )≤
)≤
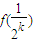 -2
-2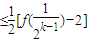 对一切k∈N*恒成立.
对一切k∈N*恒成立.
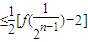
 ≤…
≤… =
= 故f(2-n)≤2-n+2(n∈N*);
故f(2-n)≤2-n+2(n∈N*); ,
,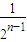 ],由f(x)是增函数,故f(x)≤f(
],由f(x)是增函数,故f(x)≤f( )≤
)≤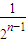 +2
+2 +2=
+2= +2,故有f(x)<2x+2
+2,故有f(x)<2x+2

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| AB |
| a2+λb2 |
| 1+λ |
| a+λb |
| 1+λ |
| log2010a+log2010b |
| 1+λ |
| a+λb |
| 1+λ |
| log2010a+log2010b |
| 1+λ |
| a+λb |
| 1+λ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、8 | B、4 | C、2 | D、1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com