
 如图,在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,M、N分别是棱DD1、D1C1的中点,则直线OM( )
如图,在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,M、N分别是棱DD1、D1C1的中点,则直线OM( )| A. | 与AC、MN均垂直相交 | B. | 与AC垂直、与MN不垂直 | ||
| C. | 与MN垂直,与AC不垂直 | D. | 与AC、MN均不垂直 |
分析 此题的条件使得建立空间坐标系方便,且选项中研究的位置关系也适合用空间向量来证明其垂直关系,故应先建立坐标系,设出边长,据几何特征,给出各点的坐标,验证向量内积是否为零
解答 解:以DA、DC、DD1所在的直线为x轴、y轴、z轴建立空间直角坐标系.如图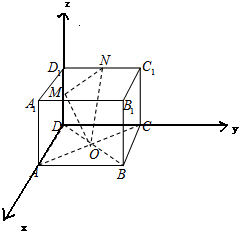
因为正方体的棱长为2,
则D(0,0,0)、D1(0,0,2)、M(0,0,1)、A(2,0,0)、C(0,2,0)、O(1,1,0)、N(0,1,2).
∴$\overrightarrow{OM}$=(-1,-1,1),$\overrightarrow{MN}$=(0,1,1),$\overrightarrow{AC}$=(-2,2,0).
∴$\overrightarrow{OM}•\overrightarrow{AC}$=0,$\overrightarrow{OM}•\overrightarrow{MN}$=0,
∴OM⊥AC,OM⊥MN.
故选A.
点评 本题考查用空间向量的方法来判断线线垂直,解答本题的关键是正确建立坐标系,使所求坐标化,利用向量的坐标运算解答.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -240 | B. | -160 | C. | 160 | D. | 240 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{x+1}$(x≥-1) | B. | y=±$\sqrt{x+1}$(x≥-1) | C. | y=-$\sqrt{x+1}$(x≥-1) | D. | y=-$\sqrt{-x+1}$(x≤1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com