
设关于 的一元二次方程
的一元二次方程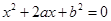 .
.
(1)若 是从
是从 、
、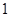 、
、 、
、 四个数中任取的一个数,
四个数中任取的一个数, 是从
是从 、
、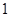 、
、 三个数中任取的一个数,求上述方程有实根的概率;
三个数中任取的一个数,求上述方程有实根的概率;
(2)若 是从区间
是从区间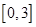 任取的一个数,
任取的一个数, 是从区间
是从区间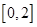 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
(1)上述方程有实根的概率为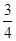 ;(2)上述方程有实根的概率为
;(2)上述方程有实根的概率为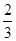 .
.
解析试题分析:(1)先将全部的基本事件以及问题中涉及事件所包含的基本事件列举出来,确定基本事件总数与问题中涉及事件所包含的基本事件的数目,然后利用古典概型的概率计算公式计算出相应事件的概率;(2)先利用方程有根这一条件转化为 ,从而确定
,从而确定 、
、 所满足的条件,然后综合
所满足的条件,然后综合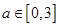 ,
,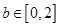 这些条件,将问题量化为平面区域的面积比的几何概型的概率来进行处理.
这些条件,将问题量化为平面区域的面积比的几何概型的概率来进行处理.
试题解析:设事件 为“方程
为“方程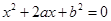 有实根”,
有实根”,
当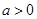 ,
, 时,方程
时,方程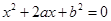 有实根的充要条件为
有实根的充要条件为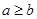 .
.
(1)基本事件共 个:
个: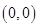 、
、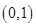 、
、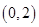 、
、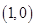 、
、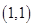 、
、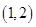 、
、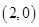 、
、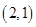 、
、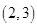 、
、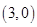 、
、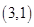 、
、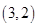 ,
,
其中第一个数表示 的取值,第二个数表示
的取值,第二个数表示 的取值.
的取值.
事件 中包含
中包含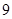 个基本事件,
个基本事件,
事件 发生的概率为
发生的概率为 ;
;
(2)试验的全部结束所构成的区域为 ,
,
构成事件 的区域为
的区域为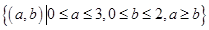 ,
,
所以所求的概率为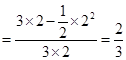 .
.
考点:古典概型与几何概型


科目:高中数学 来源: 题型:解答题
某公司计划在迎春节联欢会中设一项抽奖活动:在一个不透明的口袋中装入外形一样号码分别为1,2,3,…,10的十个小球。活动者一次从中摸出三个小球,三球号码有且仅有两个连号的为三等奖,奖金30元;三球号码都连号为二等奖,奖金60元;三球号码分别为1,5,10为一等奖,奖金240元;其余情况无奖金。
(1)求员工甲抽奖一次所得奖金ξ的分布列与期望;
(2)员工乙幸运地先后获得四次抽奖机会,他得奖次数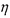 的方差是多少?
的方差是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了参加2013年东亚运动会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源如下表:
| 对别 | 北京 | 上海 | 天津 | 广州 |
| 人数 | 4 | 6 | 3 | 5 |
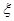 ,求随机变量
,求随机变量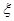 的分布列,及数学期望.
的分布列,及数学期望.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
小波以游戏方式决定:是去打球、唱歌还是去下棋.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若 就去打球;若
就去打球;若 就去唱歌;若
就去唱歌;若 就去下棋.
就去下棋.
(Ⅰ)写出数量积X的所有可能取值;
(Ⅱ)分别求小波去下棋的概率和不去唱歌的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一个盒子里装有6枝圆珠笔,其中3枝一等品,2枝二等品,1枝三等品.
(1)从盒子里任取3枝恰有1枝三等品的概率多大?;
(2)从盒子里任取3枝,设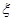 为取出的3枝里一等品的枝数,求
为取出的3枝里一等品的枝数,求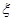 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司欲招聘员工,从1000名报名者中筛选200名参加笔试,按笔试成绩择优取50名面试,再从面试对象中聘用20名员工.
(Ⅰ)求每个报名者能被聘用的概率;
(Ⅱ)随机调查了24名笔试者的成绩如下表所示:
| 分数段 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) | [85,90) |
| 人数 | 1 | 2 | 6 | 9 | 5 | 1 |
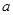 、
、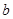 、
、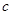 、
、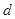 和二女
和二女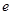 、
、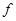 中选派两人参加某项培训,则选派结果为一男一女的概率是多少?
中选派两人参加某项培训,则选派结果为一男一女的概率是多少?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,从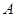 到
到 有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为
有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为 .
.
(1)当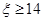 时,线路信息畅通,求线路信息畅通的概率;
时,线路信息畅通,求线路信息畅通的概率;
(2)求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排列组成.
| 第一排 | 明文字符 | A | B | C | D |
| 密码字符 | 11 | 12 | 13 | 14 | |
| 第二排 | 明文字符 | E | F | G | H |
| 密码字符 | 21 | 22 | 23 | 24 | |
| 第三排 | 明文字符 | M | N | P | Q |
| 密码字符 | 1 | 2 | 3 | 4 |
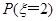 ;
;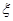 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
由于某高中建设了新校区,为了交通方便要用三辆通勤车从新校区把教师接到老校区,已知从新校区到老校区有两条公路,汽车走公路①堵车的概率为 ,不堵车的概率为
,不堵车的概率为 ;汽车走公路②堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
;汽车走公路②堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
(1)若三辆汽车中恰有一辆汽车被堵的概率为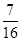 ,求走公路②堵车的概率;
,求走公路②堵车的概率;
(2)在(1)的条件下,求三辆汽车中被堵车辆的个数ξ的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com