已知数列{an}的前n项和Sn=12n-n2,求数列{|an|}的前n项和Tn.
解:当n=1时,a
1=S
1=12-1
2=11;
当n≥2时,a
n=S
n-S
n-1=12n-n
2-[12(n-1)-(n-1)
2]=13-2n.
∵n=1时适合上式,
∴{a
n}的通项公式为a
n=13-2n.
由a
n=13-2n≥0,得n≤

,
即当 1≤n≤6(n∈N
*)时,a
n>0;当n≥7时,a
n<0.
(1)当 1≤n≤6(n∈N
*)时,
T
n=|a
1|+|a
2|+…+|a
n|=a
1+a
2+…+a
n=12n-n
2.
(2)当n≥7(n∈N
*)时,
T
n=|a
1|+|a
2|+…+|a
n|=(a
1+a
2+…+a
6)-(a
7+a
8+…+a
n)=-(a
1+a
2+…+a
n)+2(a
1+…+a
6)
=-S
n+2S
6=n
2-12n+72.
∴T
n=
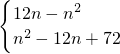
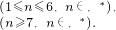
.
分析:由S
n=12n-n
2知S
n是关于n的无常数项的二次函数(n∈N
*),可知{a
n}为等差数列,求出a
n,然后再判断哪些项为正,哪些项为负,然后求解T
n.
点评:本题考查数列前n项和与通项公式的应用,考查转化思想与计算能力.

 ,
,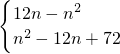
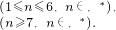 .
.

 智慧小复习系列答案
智慧小复习系列答案