已知函数f(x)=x2+2ax+2,x∈[-4,4]
(1)求实数a的取值范围,使y=f(x)在区间[-4,4]上是单调函数
(2)若函数f(x)(x∈R)的图象与直线y=-2无交点,求实数a的取值范围
(3)若函数f(x)在[-4,4]上的最小值为-16,求a的值.
解:二次函数f(x)=x
2+2ax+2的对称轴为x=-a,
(1)由于此函数在区间[-4,4]上是单调函数,
可得f(x)的对称轴落在区间[-4,4]外,
即-a≤-4或-a≥4,解得a≤-4或a≥4,
故a的取值范围是a≤-4或a≥4;
(2)若函数f(x)(x∈R)的图象与直线y=-2无交点,只需f(x)
min>-2,
又由于二次函数f(x)=x
2+2ax+2是开口向上的二次函数,
则
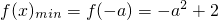
>-2,解得-2<a<2,
故实数a的取值范围是-2<a<2;
(3)①当a≤-4时,
二次函数f(x)=x
2+2ax+2在区间[-4,4]上是单调减函数,
则f(x)
min=f(4)=18+8a,解f(x)
min=-16得到
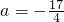
②当-4<a<4时,二次函数f(x)=x
2+2ax+2在区间[-4,4]上不是单调函数,
则
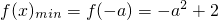
,解f(x)
min=-16得到
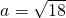
(舍)
③当a≥4时,
二次函数f(x)=x
2+2ax+2在区间[-4,4]上是单调增函数,
则f(x)
min=f(-4)=18-8a,解f(x)
min=-16得到

综上可得
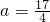
.
分析:(1)由于二次函数在区间[-4,4]上是单调函数,可得f(x)的对称轴落在区间[-4,4]外,即-a≤-4或-a≥4,解出m即可;
(2)由题意知,若函数f(x)(x∈R)的图象与直线y=-2无交点,只需f(x)
min>-2,问题转而求函数f(x)的最小值,由于f(x)是开口向上的二次函数,则
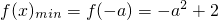
;
(3)由(1)可知,需分三种情况①当a≤-4时,②当-4<a<4时,③当a≥4时,分别求出最小值,让f(x)
min=-16,解出a即可.
点评:本题主要考察二次函数的单调性与最值,注意含参的二次函数求最值时,要对参数分类讨论.

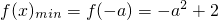 >-2,解得-2<a<2,
>-2,解得-2<a<2,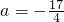
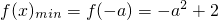 ,解f(x)min=-16得到
,解f(x)min=-16得到 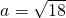 (舍)
(舍)
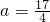 .
.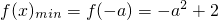 ;
;

 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<