

| 解:点A,B在抛物线y2=4px上,
设A( ∴ 由OA⊥OB,得kOA·kOB= 依点A在AB上,得直线AB方程 (yA+yB)(y-yA)=4p(x- 由OM⊥AB,得直线OM方程y= 设点M(x,y),则x,y满足②、③两式,将②式两边同时乘以- 整理得, 由③、④两式得- 由①式知,yAyB=-16p2, ∴x2+y2-4px=0. 因为A、B是原点以外的两点,所以x≠0. 所以点M的轨迹是以(2p,0)为圆心,以2p为半径的圆,去掉坐标原点. |


科目:高中数学 来源:北京高考真题 题型:解答题
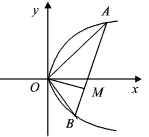
查看答案和解析>>
科目:高中数学 来源:2000年北京市高考数学试卷(理)(解析版) 题型:解答题
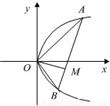
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com