
已知函数f(x)=x2+2alnx.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数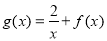 在
在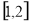 上是减函数,求实数a的取值范围.
上是减函数,求实数a的取值范围.
(Ⅰ)当a≥0时,递增区间为(0,+∞);当a<0时,递减区间是(0,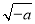 );递增区间是(
);递增区间是(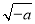 ,+∞);(Ⅱ)
,+∞);(Ⅱ)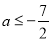 .
.
【解析】
试题分析:
解题思路:(Ⅰ)求定义域与导函数,因含有参数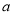 ,分类讨论求出函数的单调区间;(Ⅱ)利用“函数g(x)为[1,2]上的单调减函数,则g′(x)≤0在[1,2]上恒成立”,得到不等式恒成立;再分离参数,求函数的最值即可.
,分类讨论求出函数的单调区间;(Ⅱ)利用“函数g(x)为[1,2]上的单调减函数,则g′(x)≤0在[1,2]上恒成立”,得到不等式恒成立;再分离参数,求函数的最值即可.
规律总结:若函数 在某区间上单调递增,则
在某区间上单调递增,则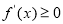 在该区间恒成立;“若函数
在该区间恒成立;“若函数 在某区间上单调递减,则
在某区间上单调递减,则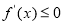 在该区间恒成立.
在该区间恒成立.
试题解析:(Ⅰ)f′(x)=2x+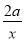 =
=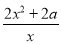 , 函数f(x)的定义域为(0,+∞).
, 函数f(x)的定义域为(0,+∞).
①当a≥0时,f′(x)>0,f(x)的单调递增区间为(0,+∞);
②当a<0时,f′(x)=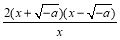 .
.
当x变化时,f′(x),f(x)的变化情况如下:
x | (0, |
| ( |
f′(x) | - | 0 | + |
f(x) |
| 极小值 |
|
由上表可知,函数f(x)的单调递减区间是(0,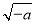 );单调递增区间是(
);单调递增区间是(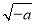 ,+∞).
,+∞).
(Ⅱ)由g(x)=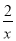 +x2+2aln x,得g′(x)=-
+x2+2aln x,得g′(x)=-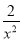 +2x+
+2x+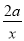 ,
,
由已知函数g(x)为[1,2]上的单调减函数,则g′(x)≤0在[1,2]上恒成立,
即-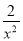 +2x+
+2x+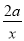 ≤0在[1,2]上恒成立.即a≤
≤0在[1,2]上恒成立.即a≤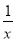 -x2在[1,2]上恒成立.
-x2在[1,2]上恒成立.
令h(x)=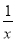 -x2,在[1,2]上h′(x)=-
-x2,在[1,2]上h′(x)=-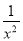 -2x=-(
-2x=-(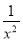 +2x)<0,
+2x)<0,
所以h(x)在[1,2]上为减函数,h(x)min=h(2)=-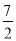 ,所以a≤-
,所以a≤-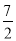 .
.
故实数a的取值范围为{a|a≤-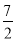 }.
}.
考点:1.利用导数求函数的单调区间;2.根据函数的单调性求参数.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源:2015届山东省高二暑假作业四数学试卷(解析版) 题型:填空题
二维空间中圆的一维测度(周长) ,二维测度(面积)
,二维测度(面积) ,观察发现
,观察发现 ;三维空间中球的二维测度(表面积)
;三维空间中球的二维测度(表面积) ,三维测度(体积)
,三维测度(体积) ,观察发现
,观察发现 .已知四维空间中“超球”的三维测度
.已知四维空间中“超球”的三维测度 ,猜想其四维测度
,猜想其四维测度 ________.
________.
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二暑假作业二数学试卷(解析版) 题型:填空题
某产品的广告费用 与销售额
与销售额 的统计数据如下表:
的统计数据如下表:
广告费用 | 3 | 4 | 5 | 6 |
销售额 | 25 | 30 | 40 | 45 |
根据上表可得回归方程 中的
中的 为7.据此模型预报广告费用为10万元时销售额为 (万元).
为7.据此模型预报广告费用为10万元时销售额为 (万元).
查看答案和解析>>
科目:高中数学 来源:2015届山东省菏泽市高二下学期期末考试理科数学试卷(解析版) 题型:填空题
已知函数f(x)=ax3+bx2+cx+d的图象与x轴有三个不同交点(0,0),(x1,0),(x2,0),且f(x)在x=1,x=2时取得极值,则x1•x2的值为 .
查看答案和解析>>
科目:高中数学 来源:2015届山东省菏泽市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
我国第一艘航母“辽宁舰”在某次舰载机起降飞行训练中,有5架歼﹣15飞机准备着舰.如果甲、乙两机必须相邻着舰,而丙、丁两机不能相邻着舰,那么不同的着舰方法有( ).
A.12 B.18 C.24 D.48
查看答案和解析>>
科目:高中数学 来源:2015届山东省菏泽市高二下学期期末考试文科数学试卷(解析版) 题型:填空题
已知物体的运动方程为s=t2+ (t是时间,s是位移),则物体在时刻t=2时的速度为 .
(t是时间,s是位移),则物体在时刻t=2时的速度为 .
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期中考试理科数学试卷(解析版) 题型:填空题
长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com