
分析 (1)当a=2时,利用导数的符号求得函数的单调性,再根据函数的单调性求得函数y=f(x)在$[\frac{1}{2},2]$上的最大值.
(2)由题意可得,f(x)-mx=0有两个实根x1,x2,化简可得$m=\frac{{2(ln{x_1}-ln{x_2})}}{{{x_1}-{x_2}}}-({x_1}+{x_2})$.可得h′(αx1+βx2)=$\frac{2}{{α{x_1}+β{x_2}}}-\frac{{2(ln{x_1}-ln{x_2})}}{{{x_1}-{x_2}}}+(2α-1)({x_2}-{x_1})$,由条件知(2α-1)(x2-x1)≤0,再用分析法证明h′(αx1+βx2)<0.
解答 解:(1)∵函数f(x)=alnx-x2 ,可得当a=2时,${f^'}(x)=\frac{2}{x}-2x=\frac{{2-2{x^2}}}{x}$,…(2分)
故函数y=f(x)在[$\frac{1}{2}$,1]是增函数,在[1,2]是减函数,
所以$f{(x)_{max}}=f(1)=2ln1-{1^2}=-1$. …(4分)
(2)h′(αx1+βx2)<0可以恒成立.
证明:由题意可得,${h^'}(x)=\frac{2}{x}-2x-m$,又f(x)-mx=0有两个实根x1,x2,
∴$\left\{{\begin{array}{l}{2ln{x_1}-x_1^2-m{x_1}=0}\\{2ln{x_2}-x_2^2-m{x_2}=0}\end{array}}\right.$,两式相减,得$2(ln{x_1}-ln{x_2})-({x_1}^2-x_2^2)=m({x_1}-{x_2})$,
∴$m=\frac{{2(ln{x_1}-ln{x_2})}}{{{x_1}-{x_2}}}-({x_1}+{x_2})$.…(6分)
于是${h^'}(α{x_1}+β{x_2})=\frac{2}{{α{x_1}+β{x_2}}}-2(α{x_1}+β{x_2})-\frac{{2(ln{x_1}-ln{x_2})}}{{{x_1}-{x_2}}}+({x_1}+{x_2})$=$\frac{2}{{α{x_1}+β{x_2}}}-\frac{{2(ln{x_1}-ln{x_2})}}{{{x_1}-{x_2}}}+(2α-1)({x_2}-{x_1})$ …(8分)
∵β≥α,∴2α≤1,
∴(2α-1)(x2-x1)≤0.
要证:h′(αx1+βx2)<0,只需证:$\frac{2}{{α{x_1}+β{x_2}}}-\frac{{2(ln{x_1}-ln{x_2})}}{{{x_1}-{x_2}}}<0$,
只需证:$\frac{{{x_1}-{x_2}}}{{α{x_1}+β{x_2}}}-ln\frac{x_1}{x_2}>0$.(*) …(10分)
令$\frac{x_1}{x_2}=t∈(0,1)$,∴(*)化为 $\frac{1-t}{αt+β}+lnt<0$,只证$u(t)=lnt+\frac{1-t}{αt+β}<0$即可.…(11分)
∵${u^'}(t)=\frac{1}{t}+\frac{-(αt+β)-(1-t)α}{{{{(αt+β)}^2}}}=\frac{1}{t}-\frac{1}{{{{(αt+β)}^2}}}=\frac{{{{(αt+β)}^2}-t}}{{t{{(αt+β)}^2}}}=\frac{{{α^2}(t-1)(t-\frac{β^2}{α^2})}}{{t{{(αt+β)}^2}}}$,…(12分)
又∵$\frac{β^2}{α^2}≥1,0<t<1$,
∴t-1<0,∴u′(t)>0,
∴u(t)在(0,1)上单调递增,…(13分)
故有 u(t)<u(1)=0,
∴$lnt+\frac{1-t}{αt+β}<0$,即$\frac{{{x_1}-{x_2}}}{αt+β}+ln\frac{x_1}{x_2}<0$.
∴h′(αx1+βx2)<0恒成立.…(14分)
点评 本题主要考查利用导数研究函数的单调性,利用函数的单调性求函数在闭区间上的最值,用分析法证明不等式,体现了转化的数学思想,属于难题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源:2017届广东华南师大附中高三综合测试一数学(理)试卷(解析版) 题型:解答题
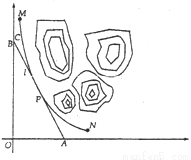
某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路和山区边界的直线型公路.记两条相互垂直的公路为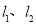 ,山区边界曲线为
,山区边界曲线为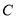 .计划修建的公路为
.计划修建的公路为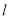 ,如图所示,
,如图所示,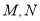 为
为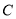 的两个端点,测得点
的两个端点,测得点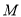 到
到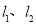 的距离分别为5千米和40千米,点
的距离分别为5千米和40千米,点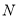 到
到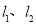 的距离分别为20千米和2.5千米,以
的距离分别为20千米和2.5千米,以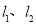 所在直线分别为
所在直线分别为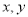 轴,建立平面直角坐标系
轴,建立平面直角坐标系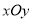 .假设曲线
.假设曲线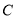 符合函数
符合函数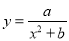 (其中
(其中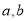 为常数)模型.
为常数)模型.
(1)求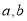 的值;
的值;
(2)设公路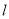 与曲线
与曲线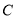 相切于
相切于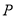 点,
点,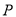 的横坐标为
的横坐标为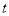 .
.
①请写出公路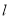 长度的函数解析式
长度的函数解析式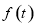 ,并写出其定义域;
,并写出其定义域;
②当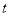 为何值时,公路
为何值时,公路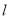 的长度最短?求出最短长度.
的长度最短?求出最短长度.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{π}{2}$]∪[$\frac{3π}{4}$,π) | B. | [0,$\frac{π}{2}$)∪($\frac{π}{2}$,$\frac{3π}{4}$) | C. | [$\frac{π}{4}$,$\frac{π}{2}$] | D. | [$\frac{3π}{4}$,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com