
 如图,多面体ABCDEF中,DE⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°,四边形BDEF是正方形.
如图,多面体ABCDEF中,DE⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°,四边形BDEF是正方形.分析 (Ⅰ)取EF的中点O,连接AO,CO,AC,推导出AO⊥EF,CO⊥EF,从而∠AOC为二面角A-EF-C的平面角,由此能求出二面角A-EF-C的余弦值.
(Ⅱ)作AH⊥CO交CO于H点,则AH⊥平面CEF,∠AFH是直线AF与平面ECF所成角,由此能求出直线AF与平面ECF所成角的正弦值.
(Ⅲ)A在平面CEF上的射影在中线CO上(不在C点),由此得到在线段EC上不存在点P,使得AP⊥平面CEF.
解答  证明:(Ⅰ)取EF的中点O,连接AO,CO,AC.
证明:(Ⅰ)取EF的中点O,连接AO,CO,AC.
由题可知:
AE=AF=CF=CE=2$\sqrt{2}$,EF=2
所以AO⊥EF,CO⊥EF,则∠AOC为二面角A-EF-C的平面角.
在△AOC中,AC=2$\sqrt{3}$,cos∠AOC=$\frac{A{O}^{2}+C{O}^{2}-A{C}^{2}}{2AO•CO}$=$\frac{1}{7}$,
故二面角A-EF-C的余弦值为$\frac{1}{7}$ ….…..(4分)
解:(Ⅱ)∵DE⊥平面ABCD,底面ABCD是菱形,四边形BDEF是正方形,
∴DE⊥AC,BD⊥AC,∴AC⊥EF,
∵AE=AF,O是EF中点,∴AO⊥EF,
∵AC∩AO=A,∴EF⊥平面AOC,
∴EF?平面CEF,
作AH⊥CO交CO于H点,则AH⊥平面CEF,
∴∠AFH是直线AF与平面ECF所成角,
直线AF与平面ECF所成角的正弦值:
sin∠AFH=$\frac{AH}{AF}$=$\frac{\frac{4\sqrt{21}}{7}}{2\sqrt{2}}$=$\frac{\sqrt{42}}{7}$.….…..(8分)
(Ⅲ)不存在
由第二问知:A在平面CEF上的射影在中线CO上(不在C点),
而过一点作已知平面的垂线只能作一条,
故在线段EC上不存在点P,使得AP⊥平面CEF.….…..(12分)
点评 本题考查二面角的余弦值的求法,考查线面角的正弦值的求法,考查满足线面垂直的点是否存在的判断与求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
| A. | -7 | B. | -14 | C. | 7 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 18 | C. | 16 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a|c|>b|c| | B. | ac2>bc2 | C. | a2c>b2c | D. | $\frac{1}{a}$<$\frac{1}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 做不到光盘 | 能做到光盘 | 合计 | |
| 男 | 45 | 10 | 55 |
| 女 | x | y | 45 |
| 合计 | 75 | m | 100 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
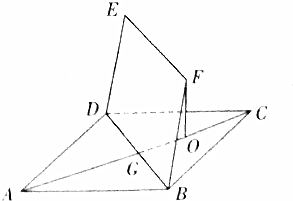 如图,正方形ABCD的边长为2$\sqrt{2}$,四边形BDEF是平行四边形,BD与AC交于点G,O为GC的中点,且FO⊥平面ABCD,FO=$\sqrt{3}$.
如图,正方形ABCD的边长为2$\sqrt{2}$,四边形BDEF是平行四边形,BD与AC交于点G,O为GC的中点,且FO⊥平面ABCD,FO=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 100 | B. | 92 | C. | 88 | D. | 72 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1) | B. | [0,2) | C. | [0,3) | D. | [0,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com