


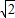 sin(x+
sin(x+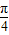 ),其最小正周期T=2π;
),其最小正周期T=2π;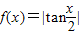 ,先去掉绝对值,利用正切的周期公式得到f(x)=tan
,先去掉绝对值,利用正切的周期公式得到f(x)=tan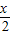 ,其最小正周期T=2π;
,其最小正周期T=2π;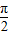
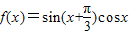 =(
=( sinx+
sinx+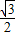 cosx)cosx=
cosx)cosx= sin2x+
sin2x+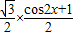
 sin2x+
sin2x+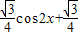 =
= sin(2x+
sin(2x+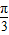 )+
)+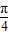 ,
,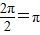
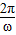 ,正切型最小正周期为T=
,正切型最小正周期为T=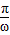 ,初次之外可以用图象法,定义法,公倍数法,对于具体问题得具体分析.求三角函数的周期,要注意函数的三角变换,得到可以利用三角函数的周期公式来求解的形式,本题是一个中档题目.
,初次之外可以用图象法,定义法,公倍数法,对于具体问题得具体分析.求三角函数的周期,要注意函数的三角变换,得到可以利用三角函数的周期公式来求解的形式,本题是一个中档题目. 

 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源:2010-2011学年山东省济南国语学校高一(下)期末数学试卷(解析版) 题型:选择题
 上是增函数的是( )
上是增函数的是( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com