
| A. | ${log}_{\frac{1}{2}}$t<1<t | B. | t<1<${log}_{\frac{1}{2}}$t | C. | ${log}_{\frac{1}{2}}$t<t<1 | D. | t<${log}_{\frac{1}{2}}$t<1 |
分析 ?t∈R,2t>0,log2t<0,可得0<t<1.画出图象:(t用x代换).y=-2x,y=log2x.当$0<x<\frac{1}{2}$时;当$\frac{1}{2}≤x<1$时.可得$0<t<\frac{1}{2}$,即可得出.
解答 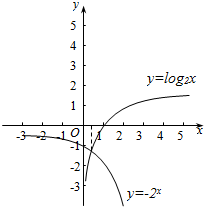 解:∵?t∈R,2t>0,∴log2t<0,∴0<t<1.
解:∵?t∈R,2t>0,∴log2t<0,∴0<t<1.
画出图象:
(t用x代换).
y=-2x,y=log2x.
当$0<x<\frac{1}{2}$时,$-\sqrt{2}<-{2}^{x}<-1$,log2x<-1;
当$\frac{1}{2}≤x<1$时,$-{2}^{x}≤-\sqrt{2}$,log2x≥-1.
∴$0<t<\frac{1}{2}$,
∴log2t<-1,∴$lo{g}_{\frac{1}{2}}t$>1,
故$t<1<lo{g}_{\frac{1}{2}}t$.
故选:B.
点评 本题考查了指数函数与对数的图象与性质,考查了推理能力与计算能力,属于中档题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,0)∪(0,+∞) | D. | R |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | a>b>c | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-∞,-1] | C. | [-3,-1] | D. | [-3,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
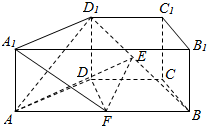 如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2DC=2,E为BD1的中点,F为AB的中点,∠DAB=60°.
如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2DC=2,E为BD1的中点,F为AB的中点,∠DAB=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com