已知函数f(x)=x3-bx2+2cx的导函数的图象关于直线x=2对称.
(1)求b的值;
(2)若函数f(x)无极值求c的取值范围;
(3)若f(x)在x=t处取得极小值,记此极小值为g(t),求g(t)的定义域和值域.
解:(1)f'(x)=3x
2-2bx+2c…(1分)
∵函数f'(x)的图象关于直线x=2对称,
∴-
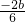
=2,即b=6.…(4分)
(2)由(1)知,f(x)=x
3-6x
2+2cx,f'(x)=3x
2-12x+2c=3(x-2)
2+2c-12…(6分)
当c≥6时,f'(x)≥0,此时f(x)无极值 …(8分)
(3)当c<6时,f'(x)=0有两个异实根x
1,x
2,不妨设x
1<x
2,则x
1<2<x
2;
当x<x
1时,f'(x)>0,f(x)在区间(-∞,x
1)内为增函数;
当x
1<x<x
2时,f'(x)<0,f(x)在区间(x
1,x
2)内为减函数;
当x>x
2时,f'(x)>0,f(x)在区间(x
2,+∞)内为增函数.
所以f(x)在x=x
1处取极大值,在x=x
2处取极小值 …(10分)
因此,当且仅当c<6时,函数f(x)在x=x
2处存在唯一极小值,所以t=x
2>2
于是g(t)的定义域为(2,+∞),由f'(t)=3t
2-12t+2c=0得2c=-3t
2+12t.
于是g(t)=f(t)=t
3-6t
2+(-3t
2+12t)t=-2t
3+6t
2,t∈(2,+∞)…(12分)
当t>2时,g'(t)=-6t
2+12t=-6t(t-2)<0,所以函数g(t)在区间(2,+∞)内是减函数,
故g(t)的值域为(-∞,8).…(14分)
分析:(1)先求导函数,根据导函数的图象关于直线x=2对称,可知-
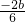
=2,从而可求b的值;
(2)函数f(x)无极值,即导函数为0的方程至多有一解,从而可求c的取值范围;
(3)由(2)知,c<6,f'(x)=0有两个异实根x
1,x
2,不妨设x
1<x
2,则x
1<2<x
2,易得f(x)在x=x
1处取极大值,在x=x
2处取极小值,且x
2>2,可知函数g(t)的定义域为(2,+∞),根据f'(t)=3t
2-12t+2c=0得2c=-3t
2+12t.从而可得g(t)=f(t)=t
3-6t
2+(-3t
2+12t)t=-2t
3+6t
2,再利用函数g(t)在区间(2,+∞)内是减函数,可求函数g(t)的值域.
点评:本题以导函数为载体,考查导函数的性质,考查利用导数求函数的极值,同时考查了函数的定义域与值域,综合性强.

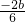 =2,即b=6.…(4分)
=2,即b=6.…(4分)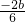 =2,从而可求b的值;
=2,从而可求b的值;

 口算能手系列答案
口算能手系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<