
已知函数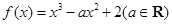 ,
,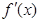 为
为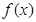 的导函数。 (1)求函数
的导函数。 (1)求函数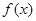 的单调递减区间;
的单调递减区间;
(2)若对一切的实数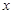 ,有
,有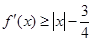 成立,求
成立,求 的取值范围;
的取值范围;
(3)当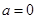 时,在曲线
时,在曲线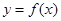 上是否存在两点
上是否存在两点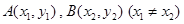 ,使得曲线在
,使得曲线在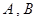 两点处的切线均与直线
两点处的切线均与直线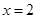 交于同一点?若存在,求出交点纵坐标的最大值;若不存在,请说明理由.
交于同一点?若存在,求出交点纵坐标的最大值;若不存在,请说明理由.
(1)当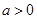 时,
时,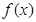 的减区间为
的减区间为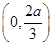 ;当
;当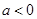 时,
时,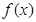 的减区间为
的减区间为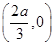 ; 当
; 当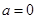 时,
时,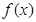 无减区间.(2)
无减区间.(2) (3)存在,且交点纵坐标的最大值为10.
(3)存在,且交点纵坐标的最大值为10.
解析试题分析:(1)首先对函数求导,然后根据导数的性质,求原函数的单调区间.
(2)由题意可知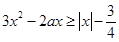 恒成立,根据绝对值的几何意义,分类去掉绝对值符号,然后再根据基本不等式求解即可.
恒成立,根据绝对值的几何意义,分类去掉绝对值符号,然后再根据基本不等式求解即可.
(3)设切线与直线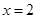 的公共点为P(2,t),当
的公共点为P(2,t),当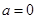 时,则
时,则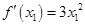 ,由导数的几何意义可知点A为切点的切线的斜率k=
,由导数的几何意义可知点A为切点的切线的斜率k=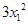 ,切线方程为
,切线方程为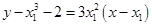 .把点P(2,t)代入切线方程
.把点P(2,t)代入切线方程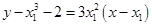 中,整理得
中,整理得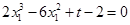 ,同理可得
,同理可得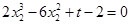 ,设
,设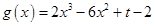 ,则原问题等价于函数
,则原问题等价于函数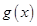 至少有两个不同的零点.求
至少有两个不同的零点.求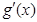 ,利用导数的性质求出函数g(x)的单调区间和极值,欲使
,利用导数的性质求出函数g(x)的单调区间和极值,欲使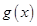 至少有两个不同的零点,则需满足极大值g(0)≥0且极小值g(2)≤0,解出t即可.
至少有两个不同的零点,则需满足极大值g(0)≥0且极小值g(2)≤0,解出t即可.
(1)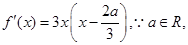 当
当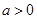 时,
时,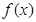 的减区间为
的减区间为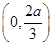 ;
;
当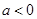 时,
时,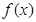 的减区间为
的减区间为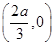 ; 当
; 当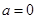 时,
时,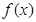 无减区间。 4分
无减区间。 4分
(2)由条件得: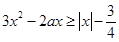 ,
,
当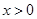 时,得
时,得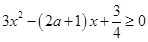 ,即
,即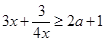 恒成立,因为
恒成立,因为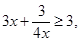
(当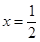 时等号成立),所以
时等号成立),所以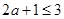 ,即
,即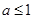 ; 6分
; 6分
当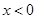 时,得
时,得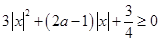 ,即
,即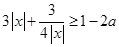 恒成立,因为
恒成立,因为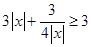 ,(当
,(当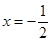 时等号成立),所以
时等号成立),所以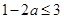 ,即
,即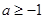 ;
;
当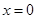 时,
时,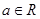 ;
;
综上所述, 的取值范围是
的取值范围是 9分
9分
(3)设切线与直线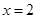 的公共点为
的公共点为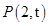 ,当
,当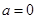 时,
时,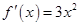 ,
,
则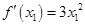 ,因此以点
,因此以点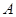 为切点的切线方程为
为切点的切线方程为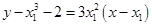 .
.
因为点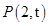 在切线上,所以
在切线上,所以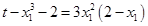 ,即
,即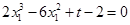 .
.
同理可得方程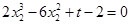 . 11分
. 11分
设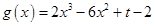 ,则原问题等价于函数
,则原问题等价于函数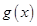 至少有两个不同的零点.
至少有两个不同的零点.
因为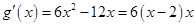


科目:高中数学 来源: 题型:解答题
已知函数f(x)=sinx,g(x)=mx-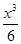 (m为实数).
(m为实数).
(1)求曲线y=f(x)在点P(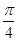 ),f(
),f(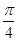 )处的切线方程;
)处的切线方程;
(2)求函数g(x)的单调递减区间;
(3)若m=1,证明:当x>0时,f(x)<g(x)+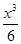 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=x3-ax2-3x.
(1)若f(x)在[1,+∞)上是增函数,求实数a的取值范围;
(2)若x=3是f(x)的极值点,求f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(14分)(2011•福建)已知a,b为常数,且a≠0,函数f(x)=﹣ax+b+axlnx,f(e)=2(e=2.71828…是自然对数的底数).
(I)求实数b的值;
(II)求函数f(x)的单调区间;
(III)当a=1时,是否同时存在实数m和M(m<M),使得对每一个t∈[m,M],直线y=t与曲线y=f(x)(x∈[ ,e])都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.
,e])都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知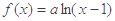 ,
,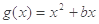 ,
,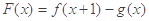 ,其中
,其中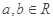 。
。
(1)若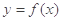 与
与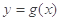 的图像在交点(2,
的图像在交点(2,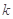 )处的切线互相垂直,
)处的切线互相垂直,
求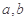 的值;
的值;
(2)若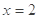 是函数
是函数 的一个极值点,
的一个极值点,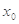 和1是
和1是 的两个零点,
的两个零点,
且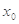 ∈(
∈(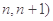
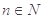 ,求
,求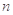 ;
;
(3)当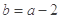 时,若
时,若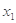 ,
,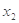 是
是 的两个极值点,当|
的两个极值点,当|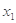 -
-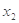 |>1时,
|>1时,
求证:|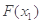 -
-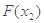 |
|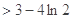
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com