练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆C：（）的离心率为，左、右焦点分别为，，过的直线与C交于M，N两点，的周长为.

    （1）求椭圆C的标准方程；

    （2）过M作与y轴垂直的直线l，点，试问直线与直线l交点的横坐标是否为定值？请说明理由.

    【答案】（1）；（2）为定值2，理由见解析

    【解析】

    （1）由离心率和过焦点的三角形的周长及a，b，c之间的关系求出a，b的值，进而求出椭圆的方程；

    （2）由（1）可得直线的方程，与椭圆联立求出两根之和及两根之积，求出的方程令，求出x的表达式，将两根之和及两根之积代入可得为定值2，

    解：（1）三角形的周长，，，可得：，，

    所以椭圆的方程为：；

    （2）设，，

    由（1）得，设直线的直线为：，

    联立直线与椭圆的方程：，解得：，

    ∴，，

    直线的方程：，令，可得：

    所以直线与直线l交点的横坐标为定值2.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在党中央的正确领导下，通过全国人民的齐心协力，特别是全体一线医护人员的奋力救治，二月份“新冠肺炎”疫情得到了控制．甲、乙两个地区采取防护措施后，统计了从2月7日到2月13日一周的新增“新冠肺炎”确诊人数，绘制成如下折线图：

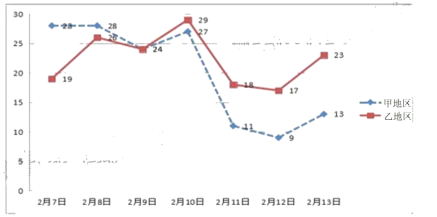
    （1）根据图中甲、乙两个地区折线图的信息，写出你认为最重要的两个统计结论；

    （2）治疗“新冠肺炎”药品的研发成了当务之急，某药企计划对甲地区的项目或乙地区的项目投入研发资金，经过评估，对于项目，每投资十万元，一年后利润是l.38万元、1.18万元、l.14万元的概率分别为、、；对于项目，利润与产品价格的调整有关，已知项目产品价格在一年内进行2次独立的调整，每次价格调整中，产品价格下调的概率都是，记项目一年内产品价格的下调次数为，每投资十万元，取0、1、2时，一年后相应利润是1.4万元、1.25万元、0.6万元．记对项目投资十万元，一年后利润的随机变量为，记对项目投资十万元，一年后利润的随机变量为．

    (i)求，的概率分布列和数学期望，；

    (ii)如果你是投资决策者，将做出怎样的决策?请写出决策理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右焦点分别为，是椭圆上一动点（与左、右顶点不重合）已知的内切圆半径的最大值为，椭圆的离心率为.

    （1）求椭圆C的方程；

    （2）过的直线交椭圆于两点，过作轴的垂线交椭圆与另一点（不与重合）.设的外心为，求证为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三棱柱中，，侧面底面，D是棱的中点.

    （1）求证：平面平面；

    （2）若，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】过抛物线的焦点F且倾斜角为的直线交抛物线于AB两点，交其准线于点C，且|AF|=|FC|，|BC|=2.

    （1）求抛物线C的方程；

    （2）直线l交抛物线C于DE两点，且这两点位于x轴两侧，与x轴交于点M，若·求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设抛物线的焦点为，准线为，为抛物线过焦点的弦，已知以为直径的圆与相切于点.

    （1）求的值及圆的方程；

    （2）设为上任意一点，过点作的切线，切点为，证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近年来，某市为了促进生活垃圾的分类处理，将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类，并分别设置了相应的垃圾箱．为调查居民生活垃圾分类投放情况，现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾，数据统计如下（单位：吨）：


    “厨余垃圾”箱

    “可回收物”箱

    “其他垃圾”箱

    厨余垃圾

    400

    100

    100

    可回收物

    30

    240

    30

    其他垃圾

    20

    20

    60

    （Ⅰ）试估计厨余垃圾投放正确的概率

    （Ⅱ）试估计生活垃圾投放错误的概率

    （Ⅲ）假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0，a+b+c=600.当数据a,b,c,的方差最大时，写出a,b,c的值（结论不要求证明），并求此时的值．

    （注：，其中为数据的平均数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解甲、乙两个快递公司的工作状况，假设同一个公司快递员的工作状况基本相同，现从甲、乙两公司各随机抽取一名快递员，并从两人某月（30天）的快递件数记录结果中随机抽取10天的数据，制表如图：

    每名快递员完成一件货物投递可获得的劳务费情况如下：甲公司规定每件4.5元；乙公司规定每天35件以内（含35件）的部分每件4元，超出35件的部分每件7元.

    （1）根据表中数据写出甲公司员工A在这10天投递的快递件数的平均数和众数；

    （2）为了解乙公司员工B的每天所得劳务费的情况，从这10天中随机抽取1天，他所得的劳务费记为X（单位：元），求X的分布列和数学期望；

    （3）根据表中数据估算两公司的每位员工在该月所得的劳务费.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设为正整数，区间（其中，）同时满足下列两个条件：

    ①对任意，存在使得；

    ②对任意，存在，使得（其中）．

    （Ⅰ）判断能否等于或；（结论不需要证明）．

    （Ⅱ）求的最小值；

    （Ⅲ）研究是否存在最大值，若存在，求出的最大值；若不在在，说明理由．

    查看答案和解析>>

    同步练习册答案