
【题目】设![]() 为正整数,区间
为正整数,区间![]() (其中
(其中![]() ,
,![]() )同时满足下列两个条件:
)同时满足下列两个条件:
①对任意![]() ,存在
,存在![]() 使得
使得![]() ;
;
②对任意![]() ,存在
,存在![]() ,使得
,使得![]() (其中
(其中![]() ).
).
(Ⅰ)判断![]() 能否等于
能否等于![]() 或
或![]() ;(结论不需要证明).
;(结论不需要证明).
(Ⅱ)求![]() 的最小值;
的最小值;
(Ⅲ)研究![]() 是否存在最大值,若存在,求出
是否存在最大值,若存在,求出![]() 的最大值;若不在在,说明理由.
的最大值;若不在在,说明理由.
【答案】(Ⅰ)![]() 可以等于
可以等于![]() ,但
,但![]() 不能等于
不能等于![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() 存在最大值,为
存在最大值,为![]() .
.
【解析】
(Ⅰ)根据题意可得出结论;
(Ⅱ)根据(Ⅰ)中的结论得出![]() 可以等于
可以等于![]() ,可得出区间
,可得出区间![]() 的长度为
的长度为![]() ,结合①得出
,结合①得出![]() ,再由
,再由![]() ,
,![]() ,
,![]() ,
,![]() 满足条件①、②可得出
满足条件①、②可得出![]() 的最小值;
的最小值;
(Ⅲ)利用反证法推导出![]() ,进而得出
,进而得出![]() ,由此得出
,由此得出![]() ,进而得出
,进而得出![]() ,再举例说明
,再举例说明![]() 成立,由此可得出正整数
成立,由此可得出正整数![]() 的最大值.
的最大值.
(Ⅰ)![]() 可以等于
可以等于![]() ,但
,但![]() 不能等于
不能等于![]() ;
;
(Ⅱ)记![]() 为区间
为区间![]() 的长度,则区间
的长度,则区间![]() 的长度为
的长度为![]() ,
,![]() 的长度为
的长度为![]() .
.
由①,得![]() .
.
又因为![]() ,
,![]() ,
,![]() ,
,![]() 显然满足条件①,②.
显然满足条件①,②.
所以![]() 的最小值为
的最小值为![]() ;
;
(Ⅲ)![]() 的最大值存在,且为
的最大值存在,且为![]() .
.
解答如下:(1)首先,证明![]() .
.
由②,得![]() 、
、![]() 、
、![]() 、
、![]() 互不相同,且对于任意
互不相同,且对于任意![]() ,
,![]() .
.
不妨设![]() .
.
如果![]() ,那么对于条件②,当
,那么对于条件②,当![]() 时,不存在
时,不存在![]() ,使得
,使得![]() .
.
这与题意不符,故![]() .
.
如果![]() ,那么
,那么![]() ,
,
这与条件②中“存在![]() ,使得
,使得![]() (其中
(其中![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() )”矛盾,故
)”矛盾,故![]() .
.
所以![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
故![]() .
.
若存在![]() ,这与条件②中“存在
,这与条件②中“存在![]() ,使得
,使得![]() ”矛盾,
”矛盾,
所以![]() .
.
(2)给出![]() 存在的例子 .
存在的例子 .
令![]() ,其中
,其中![]() 、
、![]() 、
、![]() 、
、![]() ,即
,即![]() 、
、![]() 、
、![]() 、
、![]() 为等差数列,公差
为等差数列,公差![]() .
.
由![]() ,知
,知![]() ,则易得
,则易得![]() ,
,
所以![]() 、
、![]() 、
、![]() 、
、![]() 满足条件①.
满足条件①.
又公差![]() ,
,
所以![]() ,
,![]() .(注:
.(注:![]()
为区间![]() 的中点对应的数)
的中点对应的数)
所以![]() 、
、![]() 、
、![]() 、
、![]() 满足条件②.
满足条件②.
综合(1)(2)可知![]() 的最大值存在,且为
的最大值存在,且为![]() .
.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的离心率为
)的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,过
,过![]() 的直线与C交于M,N两点,
的直线与C交于M,N两点,![]() 的周长为
的周长为![]() .
.
(1)求椭圆C的标准方程;
(2)过M作与y轴垂直的直线l,点![]() ,试问直线
,试问直线![]() 与直线l交点的横坐标是否为定值?请说明理由.
与直线l交点的横坐标是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信运动,是由腾讯开发的一个类似计步数据库的公众账号.用户可以通过关注微信运动公众号查看自己每天行走的步数,同时也可以和其他用户进行运动量的![]() 或点赞.微信运动公众号为了解用户的一些情况,在微信运动用户中随机抽取了100名用户,统计了他们某一天的步数,数据整理如下:
或点赞.微信运动公众号为了解用户的一些情况,在微信运动用户中随机抽取了100名用户,统计了他们某一天的步数,数据整理如下:
|
|
|
|
|
|
|
| 5 | 20 | 50 | 15 | 5 | 5 |
(1)根据表中数据,在如图所示的坐标平面中作出其频率分布直方图,并在纵轴上标明各小长方形的高;
(2)若视频率分布为概率分布,在微信运动用户中随机抽取3人,求至少2人步数多于1.2万步的概率;
(3)若视频率分布为概率分布,在微信运动用户中随机抽取2人,其中每日走路不超过0.8万步的有![]() 人,超过1.2万步的有
人,超过1.2万步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级有400名学生参加某项体育测试,根据男女学生人数比例,使用分层抽样的方法从中抽取了100名学生,记录他们的分数,将数据分成7组:![]() ,整理得到如下频率分布直方图:
,整理得到如下频率分布直方图:
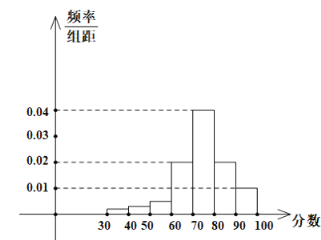
(1)若该样本中男生有55人,试估计该学校高三年级女生总人数;
(2)若规定小于60分为“不及格”,从该学校高三年级学生中随机抽取一人,估计该学生不及格的概率;
(3)若规定分数在![]() 为“良好”,
为“良好”,![]() 为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某建材商场国庆期间搞促销活动,规定:如果顾客选购物品的总金额不超过600元,则不享受任何折扣优惠;如果顾客选购物品的总金额超过600元,则超过600元部分享受一定的折扣优惠,折扣优惠按下表累计计算.
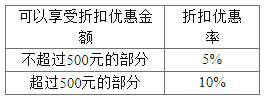
某人在此商场购物获得的折扣优惠金额为30元,则他实际所付金额为____元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国剩余定理”又称“孙子定理”,最早可见于中国南北朝时期的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”,原文如下:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?现有这样一个相关的问题:将1到2020这2020个自然数中被5除余3且被7除余2的数按照从小到大的顺序排成一列,构成一个数列,则该数列各项之和为( )
A.56383B.57171C.59189D.61242
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com