练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某建材商场国庆期间搞促销活动，规定：如果顾客选购物品的总金额不超过600元，则不享受任何折扣优惠；如果顾客选购物品的总金额超过600元，则超过600元部分享受一定的折扣优惠，折扣优惠按下表累计计算.

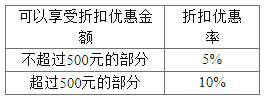
    某人在此商场购物获得的折扣优惠金额为30元，则他实际所付金额为____元．

    【答案】1120

    【解析】

    明确折扣金额y元与购物总金额x元之间的解析式，结合y＝30＞25，代入可得某人在此商场购物总金额, 减去折扣可得答案．

    由题可知：折扣金额y元与购物总金额x元之间的解析式，

    y

    ∵y＝30＞25

    ∴x＞1100

    ∴0.1（x﹣1100）+25＝30

    解得，x＝1150，

    1150﹣30＝1120，

    故此人购物实际所付金额为1120元．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设抛物线的焦点为，准线为，为抛物线过焦点的弦，已知以为直径的圆与相切于点.

    （1）求的值及圆的方程；

    （2）设为上任意一点，过点作的切线，切点为，证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】微信运动，是由腾讯开发的一个类似计步数据库的公众账号．用户可以通过关注微信运动公众号查看自己每天行走的步数，同时也可以和其他用户进行运动量的或点赞．微信运动公众号为了解用户的一些情况，在微信运动用户中随机抽取了100名用户，统计了他们某一天的步数，数据整理如下：

    (万步)

    (人)

    5

    20

    50

    15

    5

    5

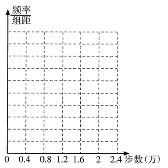
    （1）根据表中数据，在如图所示的坐标平面中作出其频率分布直方图，并在纵轴上标明各小长方形的高；

    （2）利用分层抽样的方法，从步数在（万步）中抽取7人，再从这7人中随机抽取2人，求步数在（万步）的人恰有1人的概率；

    （3）这100名用户中，的用户为男生，这些男生的步数超过1.2万步的人为20人，是否有的把握认为运动步数超过1.2万步与性别有关？

    附：

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1，在四边形中，，，，.把沿着翻折至的位置，平面，连结，如图2.

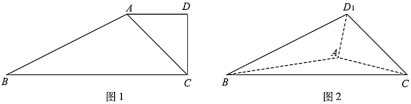
    （1）当时，证明：平面平面；

    （2）当三棱锥的体积最大时，求点到平面的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设为正整数，区间（其中，）同时满足下列两个条件：

    ①对任意，存在使得；

    ②对任意，存在，使得（其中）．

    （Ⅰ）判断能否等于或；（结论不需要证明）．

    （Ⅱ）求的最小值；

    （Ⅲ）研究是否存在最大值，若存在，求出的最大值；若不在在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为坐标原点，椭圆的右焦点为，过的直线与相交于两点，点满足.

    （1）当的倾斜角为时，求直线的方程；

    （2）试探究在轴上是否存在定点，使得为定值？若存在，求出点的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求不等式的解集；

    （2）若不等式对任意的恒成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面为正方形，平面，为线段的中点，且.

    （1）求证：平面；

    （2）求平面与平面所成锐二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在中，，.已知分别是的中点.将沿折起，使到的位置且二面角的大小是60°，连接，如图：

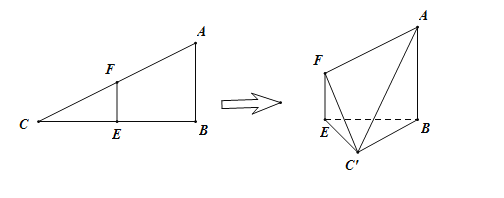
    （1）证明：平面平面

    （2）求平面与平面所成二面角的大小.

    查看答案和解析>>

    同步练习册答案