
【题目】在![]() 中,
中,![]() ,
,![]() .已知
.已知![]() 分别是
分别是![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使
折起,使![]() 到
到![]() 的位置且二面角
的位置且二面角![]() 的大小是60°,连接
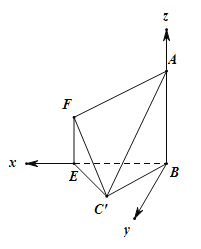
的大小是60°,连接![]() ,如图:
,如图:
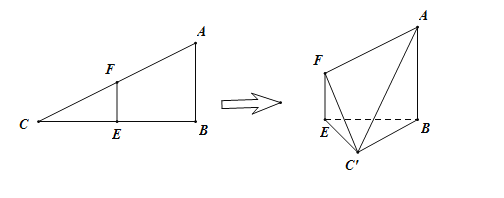
(1)证明:平面![]() 平面
平面![]()
(2)求平面![]() 与平面
与平面![]() 所成二面角的大小.
所成二面角的大小.
【答案】(1)证明见解析(2)45°
【解析】
(1)设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,设
,设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() ,从而
,从而![]() 即为二面角
即为二面角![]() 的平面角,
的平面角,![]() ,推导出
,推导出![]() ,从而
,从而![]() 平面
平面![]() ,则
,则![]() ,即
,即![]() ,进而
,进而![]() 平面
平面![]() ,推导四边形
,推导四边形![]() 为平行四边形,从而
为平行四边形,从而![]() ,
,![]() 平面
平面![]() ,由此即可得证.
,由此即可得证.
(2)以B为原点,在平面![]() 中过B作BE的垂线为x轴,BE为y轴,BA为z轴建立空间直角坐标系,利用向量法求出平面
中过B作BE的垂线为x轴,BE为y轴,BA为z轴建立空间直角坐标系,利用向量法求出平面![]() 与平面
与平面![]() 所成二面角的大小.
所成二面角的大小.
(1)∵![]() 是
是![]() 的中点,∴
的中点,∴![]() .
.
设![]() 的中点为
的中点为![]() ,连接
,连接![]() .
.
设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() .
.
易证:![]() ,
,![]() ,
,
∴![]() 即为二面角
即为二面角![]() 的平面角.
的平面角.
∴![]() ,而
,而![]() 为
为![]() 的中点.
的中点.
易知![]() ,∴
,∴![]() 为等边三角形,∴
为等边三角形,∴![]() .①
.①
∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() .
.
而![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() ,即
,即![]() .②
.②
由①②,![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 分别为
分别为![]() 的中点.
的中点.
∴四边形![]() 为平行四边形.
为平行四边形.
∴![]() ,
,![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() .
.
∴平面![]() 平面
平面![]() .
.
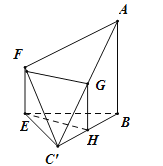
(2)如图,建立空间直角坐标系,设![]() .
.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
显然平面![]() 的法向量
的法向量![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,![]() ,
,
∴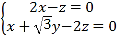 ,∴
,∴![]() .
.
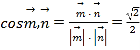 ,
,
由图形观察可知,平面![]() 与平面
与平面![]() 所成的二面角的平面角为锐角.
所成的二面角的平面角为锐角.
∴平面![]() 与平面
与平面![]() 所成的二面角大小为45°.
所成的二面角大小为45°.


科目:高中数学 来源: 题型:
【题目】某建材商场国庆期间搞促销活动,规定:如果顾客选购物品的总金额不超过600元,则不享受任何折扣优惠;如果顾客选购物品的总金额超过600元,则超过600元部分享受一定的折扣优惠,折扣优惠按下表累计计算.
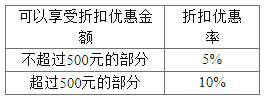
某人在此商场购物获得的折扣优惠金额为30元,则他实际所付金额为____元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从盛满2升纯酒精的容器里倒出1升纯酒精,然后填满水,再倒出1升混合溶液后又用水填满,以此继续下去,则至少应倒 次后才能使纯酒精体积与总溶液的体积之比低于10%.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国剩余定理”又称“孙子定理”,最早可见于中国南北朝时期的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”,原文如下:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?现有这样一个相关的问题:将1到2020这2020个自然数中被5除余3且被7除余2的数按照从小到大的顺序排成一列,构成一个数列,则该数列各项之和为( )
A.56383B.57171C.59189D.61242
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点![]() ,
,![]() ,抛物线
,抛物线![]() 的焦点
的焦点![]() 为线段
为线段![]() 中点.
中点.
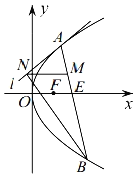
(1)求抛物线![]() 的方程;
的方程;
(2)过点![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,
两点,![]() ,过点
,过点![]() 作抛物线
作抛物线![]() 的切线
的切线![]() ,
,![]() 为切线
为切线![]() 上的点,且
上的点,且![]() 轴,求
轴,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形ABCD为平行四边形,且
中,四边形ABCD为平行四边形,且![]() ,
,![]() ,
,![]() 平面PAC.
平面PAC.

(1)求证:![]() 平面
平面![]() ;
;
(2)若异面直线PC与AD所成的角为30°,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() 的棱长为1,P是空间中任意一点,下列正确命题的个数是( )
的棱长为1,P是空间中任意一点,下列正确命题的个数是( )
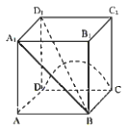
①若P为棱![]() 中点,则异面直线AP与CD所成角的正切值为
中点,则异面直线AP与CD所成角的正切值为![]() ;
;
②若P在线段![]() 上运动,则
上运动,则![]() 的最小值为
的最小值为![]() ;
;
③若P在半圆弧CD上运动,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 外接球的表面积为
外接球的表面积为![]() ;
;
④若过点P的平面![]() 与正方体每条棱所成角相等,则
与正方体每条棱所成角相等,则![]() 截此正方体所得截面面积的最大值为
截此正方体所得截面面积的最大值为![]()
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 过点
过点![]() ,且与
,且与![]() 内切,设
内切,设![]() 的圆心
的圆心![]() 的轨迹为
的轨迹为![]() ,
,
(1)求轨迹C的方程;
(2)设直线![]() 不经过点
不经过点![]() 且与曲线
且与曲线![]() 交于点
交于点![]() 两点,若直线
两点,若直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() ,判断直线
,判断直线![]() 是否过定点,若过定点,求出此定点的坐标,若不过定点,请说明理由.
是否过定点,若过定点,求出此定点的坐标,若不过定点,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com