
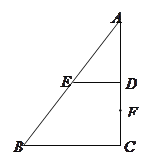
【题目】如果有一天我们分居异面直线的两头,那我一定穿越时空的阻隔,画条公垂线向你冲来,一刻也不愿逗留.如图1所示,在梯形![]() 中,
中,![]() //
//![]() ,且
,且![]() ,
,![]() ,分别延长两腰交于点
,分别延长两腰交于点![]() ,点
,点![]() 为线段
为线段![]() 上的一点,将
上的一点,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2所示.
,如图2所示.

(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() ,求四棱锥
,求四棱锥![]() 的表面积.
的表面积.
【答案】(1)见解析;(2)![]()
【解析】
⑴先证![]() 平面
平面![]() ,继而
,继而![]() ,又
,又![]() ,证得
,证得![]() 面
面![]() ,即可证得
,即可证得![]()
⑵分别计算出梯形面积和四个三角形面积即可得到表面积
(1)证明:因为∠C=90°,即AC⊥BC,且DE∥BC,

所以DE⊥AC,则DE⊥DC,DE⊥DA1,
又因为DC∩DA1=D,
所以DE⊥平面A1DC.
因为A1F平面A1DC,
所以DE⊥A1F.
又因为A1F⊥CD,CD∩DE=D,
所以A1F⊥平面BCDE,
又因为BE 平面BCDE,
所以A1F⊥BE.
(2)解:由已知DE∥BC,且DE=![]() BC,得D,E分别为AC,AB的中点,
BC,得D,E分别为AC,AB的中点,
在Rt△ABC中,![]() ,则A1E=EB=5,A1D=DC=4,
,则A1E=EB=5,A1D=DC=4,
则梯形BCDE的面积S1=![]() ×(6+3)×4=18,
×(6+3)×4=18,
四棱锥A1—BCDE的体积为V=![]() ×18×A1F=12
×18×A1F=12![]() ,即A1F=2
,即A1F=2![]() ,
,
在Rt△A1DF中,![]() ,即F是CD的中点,
,即F是CD的中点,
所以A1C=A1D=4,
因为DE∥BC,DE⊥平面A1DC,
所以BC⊥平面A1DC,所以BC⊥A1C,所以![]() ,
,
在等腰△A1BE中,底边A1B上的高为![]() ,
,
所以四棱锥A1—BCDE的表面积为
S=S1+![]() +
+![]() +
+![]()
![]()
=18+![]() ×3×4+
×3×4+![]() ×4×2
×4×2![]() +
+![]() ×6×4+
×6×4+![]() ×2
×2![]() ×2
×2![]() =36+4
=36+4![]() +2
+2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知向量a=(3sinα,cosα),b=(2sinα,5sinα-4cosα),α∈![]() ,且a⊥b.
,且a⊥b.
(1)求tanα的值;
(2)求cos![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】填空:
(1)如果![]() ,且
,且![]() ,则
,则![]() 是第________象限角;
是第________象限角;
(2)如果![]() ,且
,且![]() ,则
,则![]() 是第________象限角;
是第________象限角;
(3)如果![]() ,且
,且![]() ,则
,则![]() 是第________象限角;
是第________象限角;
(4)如果![]() ,且
,且![]() ,则
,则![]() 是第________象限角.
是第________象限角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率![]() ,数学发展史上出现过许多很有创意的求法,如著名的蒲丰试验.受其启发,我们也可以通过设计下面的试验来估计
,数学发展史上出现过许多很有创意的求法,如著名的蒲丰试验.受其启发,我们也可以通过设计下面的试验来估计![]() 的值,试验步骤如下:①先请高二年级 500名同学每人在小卡片上随机写下一个实数对
的值,试验步骤如下:①先请高二年级 500名同学每人在小卡片上随机写下一个实数对![]() ;②若卡片上的
;②若卡片上的![]() 能与1构成锐角三角形,则将此卡片上交;③统计上交的卡片数,记为
能与1构成锐角三角形,则将此卡片上交;③统计上交的卡片数,记为![]() ;④根据统计数
;④根据统计数![]() 估计
估计![]() 的值.假如本次试验的统计结果是
的值.假如本次试验的统计结果是![]() ,那么可以估计
,那么可以估计![]() 的值约为( )
的值约为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,由均匀材质制成的一个正20面体(每个面都是正三角形),将20个面平分成10组,第1组标上0,第2组标上1,…,第10组标上9.
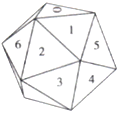
(1)投掷正20面体,若把朝上一面的数字作为投掷结果,则出现0,1,2,…,9是等可能的吗?
(2)三个正20面体分别涂上红、黄、蓝三种颜色,分别代表百位、十位、个位,同时投掷可以产生一个三位数(百位为0的也看作三位数),它是000~999范围内的随机数吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() :
: (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,且满足
上,且满足![]() ,(
,(![]() 为坐标原点).
为坐标原点).
(1)求抛物线![]() 的方程;
的方程;
(2)过点![]() 作斜率乘积为1的两条不重合的直线
作斜率乘积为1的两条不重合的直线![]() ,且
,且![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,
两点,![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,线段
两点,线段![]() 的中点分别为
的中点分别为![]() ,求证:直线
,求证:直线![]() 过定点,并求出定点坐标.
过定点,并求出定点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com