Question

已知点A（1，-2，11）、B（4，2，3），C（6，-1，4），则△ABC中角C的大小是________．

Answer 1

90°
分析：空间两点P₁（x₁，y₁，z₁），P₂（x₂，y₂，z₂），则P₁、P₂的距离：P₁P₂=，根据这个公式可以计算出AC、BC的长度，再用两个向量的夹角公式，得到∠ACB的余弦，从而得到角C的大小
解答：∵A（1，-2，11）、B（4，2，3），C（6，-1，4），
∴||==
||==
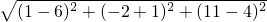
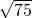
又∵，
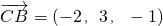
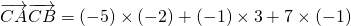
∴=0
可得cos∠ACB=
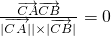
∵∠ACB∈（0°，180°）
∴∠ACB=90°
故答案为90°
点评：本题考查了空间向量的坐标运算，属于基础题．记忆空间坐标的有关公式时，同学们可以对比平面坐标里的相应公式加以联系，就不难记住了．