Question

已知z="2x" +y，x，y满足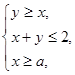且z的最大值是最小值的4倍，则a的值是      ．

Answer 1

解析试题分析：题意可得先作出不等式表示的 平面区域，由z=2x+y可得y=-2x+z，则z表示直线y=-2x+z在y轴上的截距，截距越大，z越大，可求Z的最大值与最小值，即可求解a
由题意可得，B（1，1）
∴a＜1，不等式组表示的 平面区域如图所示的△ABC
由z=2x+y可得y=-2x+z，则z表示直线y=-2x+z在y轴上的截距，截距越大，z越大
作直线L：y=-2x，把直线向可行域平移，当直线经过C时Z最小，当直线经过点B时，Z最大，由x=a,y=x，解得交点（a,a），此时Z=3a
由y=x,x+y-2=0,可得交点为B（1，1），此时z=3，故可知∴3=4×3a
∴a=故答案
考点：线性规划的最优解问题
点评：线性规划是高考重要内容，也是常考内容．此题考查该知识点增加一点变化，比较好．