
ЁОЬтФПЁПЖдгкЪ§Са![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌШєТњзу
ЃЌШєТњзу![]() ЃЌдђГЦЪ§Са
ЃЌдђГЦЪ§Са![]() ЮЊЁА
ЮЊЁА![]() Ъ§СаЁБЃЎ
Ъ§СаЁБЃЎ
ШєДцдквЛИіе§ећЪ§![]() ЃЌШєЪ§Са
ЃЌШєЪ§Са![]() жаДцдкСЌајЕФ
жаДцдкСЌајЕФ![]() ЯюКЭИУЪ§СажаСэвЛИіСЌајЕФ
ЯюКЭИУЪ§СажаСэвЛИіСЌајЕФ![]() ЯюЧЁКУАДДЮађЖдгІЯрЕШЃЌдђГЦЪ§Са
ЯюЧЁКУАДДЮађЖдгІЯрЕШЃЌдђГЦЪ§Са![]() ЪЧЁА
ЪЧЁА![]() НзПЩжиИДЪ§СаЁБЃЌ
НзПЩжиИДЪ§СаЁБЃЌ
Р§ШчЪ§Са![]() вђЮЊ
вђЮЊ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() гы
гы![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() АДДЮађЖдгІЯрЕШЃЌЫљвдЪ§Са
АДДЮађЖдгІЯрЕШЃЌЫљвдЪ§Са![]() ЪЧЁА
ЪЧЁА![]() НзПЩжиИДЪ§СаЁБЃЎ
НзПЩжиИДЪ§СаЁБЃЎ
ЃЈIЃЉЗжБ№ХаЖЯЯТСаЪ§Са![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЎЪЧЗёЪЧЁА
ЃЎЪЧЗёЪЧЁА![]() НзПЩжиИДЪ§СаЁБЃПШчЙћЪЧЃЌЧыаДГіжиИДЕФет
НзПЩжиИДЪ§СаЁБЃПШчЙћЪЧЃЌЧыаДГіжиИДЕФет![]() ЯюЃЛ
ЯюЃЛ
ЃЈIIЃЉШєЯюЪ§ЮЊ![]() ЕФЪ§Са
ЕФЪ§Са![]() вЛЖЈЪЧ ЁА
вЛЖЈЪЧ ЁА![]() НзПЩжиИДЪ§СаЁБЃЌдђ
НзПЩжиИДЪ§СаЁБЃЌдђ![]() ЕФзюаЁжЕЪЧЖрЩйЃПЫЕУїРэгЩЃЛ
ЕФзюаЁжЕЪЧЖрЩйЃПЫЕУїРэгЩЃЛ
ЃЈIIIЃЉМйЩшЪ§Са![]() ВЛЪЧЁА
ВЛЪЧЁА![]() НзПЩжиИДЪ§СаЁБЃЌШєдкЦфзюКѓвЛЯю
НзПЩжиИДЪ§СаЁБЃЌШєдкЦфзюКѓвЛЯю![]() КѓдйЬэМгвЛЯю
КѓдйЬэМгвЛЯю![]() Лђ
Лђ![]() ЃЌОљПЩ ЪЙаТЪ§СаЪЧЁА
ЃЌОљПЩ ЪЙаТЪ§СаЪЧЁА![]() НзПЩжиИДЪ§СаЁБЃЌЧв
НзПЩжиИДЪ§СаЁБЃЌЧв![]() ЃЌЧѓЪ§Са
ЃЌЧѓЪ§Са![]() ЕФзюКѓвЛЯю
ЕФзюКѓвЛЯю![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЁОД№АИЁПЃЈIЃЉ![]() ЃЛЃЈЂђЃЉ
ЃЛЃЈЂђЃЉ ![]() ЕФзюаЁжЕЪЧ
ЕФзюаЁжЕЪЧ![]() ЃЛЃЈIIIЃЉ
ЃЛЃЈIIIЃЉ![]() .
.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈIЃЉИљОнЬѕМўМАИјГіЕФаТЖЈвхХаЖЯЃЛЃЈIIЃЉНсКЯЫљИјГіЕФаТЖЈвхЃЌЗжРрЬжТлПЩЕУНсЙћЃЛЃЈIIIЃЉгУЗДжЄЗЈНјааЭЦРэЃЌПЩЕУЖј![]() ЁЃ
ЁЃ
ЪдЬтНтЮіЃК
ЃЈIЃЉ![]()
ЃЈЂђЃЉвђЮЊЪ§Са![]() ЕФУПвЛЯюжЛПЩвдЪЧ
ЕФУПвЛЯюжЛПЩвдЪЧ![]() Лђ
Лђ![]() ЃЌЫљвдСЌај
ЃЌЫљвдСЌај![]() ЯюЙВга
ЯюЙВга![]() жжВЛЭЌЕФЧщаЮЃЎ
жжВЛЭЌЕФЧщаЮЃЎ
Шє![]() ЃЌдђЪ§Са
ЃЌдђЪ§Са![]() жага
жага![]() зщСЌај
зщСЌај![]() ЯюЃЌдђетЦфжажСЩйгаСНзщАДДЮађЖдгІЯрЕШЃЌМДЯюЪ§ЮЊ
ЯюЃЌдђетЦфжажСЩйгаСНзщАДДЮађЖдгІЯрЕШЃЌМДЯюЪ§ЮЊ![]() ЕФЪ§Са
ЕФЪ§Са![]() вЛЖЈЪЧЁА
вЛЖЈЪЧЁА![]() НзПЩжиИДЪ§СаЁБЃЛ
НзПЩжиИДЪ§СаЁБЃЛ
Шє![]() ЃЌЪ§Са
ЃЌЪ§Са![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ВЛЪЧЁА
ВЛЪЧЁА![]() НзПЩжиИДЪ§СаЁБЃЛдђ
НзПЩжиИДЪ§СаЁБЃЛдђ![]() ЪБЃЌОљДцдкВЛЪЧЁА
ЪБЃЌОљДцдкВЛЪЧЁА![]() НзПЩжиИДЪ§СаЁБЕФЪ§Са
НзПЩжиИДЪ§СаЁБЕФЪ§Са![]() ЃЎ
ЃЎ
ЫљвдвЊЪЙЪ§Са![]() вЛЖЈЪЧЁА
вЛЖЈЪЧЁА![]() НзПЩжиИДЪ§СаЁБЃЌдђ
НзПЩжиИДЪ§СаЁБЃЌдђ![]() ЕФзюаЁжЕЪЧ
ЕФзюаЁжЕЪЧ![]() ЃЎ
ЃЎ
ЃЈIIIЃЉгЩгкЪ§Са![]() дкЦфзюКѓвЛЯю
дкЦфзюКѓвЛЯю![]() КѓдйЬэМгвЛЯю
КѓдйЬэМгвЛЯю![]() Лђ
Лђ![]() ЃЌОљПЩЪЙаТЪ§СаЪЧЁА
ЃЌОљПЩЪЙаТЪ§СаЪЧЁА![]() НзПЩжиИДЪ§СаЁБЃЌМДдкЪ§Са
НзПЩжиИДЪ§СаЁБЃЌМДдкЪ§Са![]() ЕФФЉЯю
ЕФФЉЯю![]() КѓдйЬэМгвЛЯю
КѓдйЬэМгвЛЯю![]() Лђ
Лђ![]() ЃЌ
ЃЌ
дђДцдк![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() гы
гы![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() АДДЮађЖдгІЯрЕШЃЌЛђ
АДДЮађЖдгІЯрЕШЃЌЛђ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() гы
гы![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() АДДЮађЖдгІЯрЕШЃЌШчЙћ
АДДЮађЖдгІЯрЕШЃЌШчЙћ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() гы
гы![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ВЛФмАДДЮађЖдгІЯрЕШЃЌ
ВЛФмАДДЮађЖдгІЯрЕШЃЌ
ФЧУДБига![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() гы
гы![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() АДДЮађЖдгІЯрЕШЃЎ
АДДЮађЖдгІЯрЕШЃЎ
ДЫЪБПМТЧ![]() ЃЌ
ЃЌ ![]() КЭ
КЭ![]() ЃЌЦфжаБигаСНИіЯрЭЌЃЌетОЭЕМжТЪ§Са
ЃЌЦфжаБигаСНИіЯрЭЌЃЌетОЭЕМжТЪ§Са![]() жагаСНИіСЌајЕФЮхЯюЧЁАДДЮађЖдгІЯрЕШЃЌДгЖјЪ§Са
жагаСНИіСЌајЕФЮхЯюЧЁАДДЮађЖдгІЯрЕШЃЌДгЖјЪ§Са![]() ЪЧЁА
ЪЧЁА![]() НзПЩжиИДЪ§СаЁБЃЌетКЭЬтЩшжаЪ§Са
НзПЩжиИДЪ§СаЁБЃЌетКЭЬтЩшжаЪ§Са![]() ВЛЪЧЁА
ВЛЪЧЁА![]() НзПЩжиИДЪ§СаЁБУЌЖмЃЁ
НзПЩжиИДЪ§СаЁБУЌЖмЃЁ
Ыљвд![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() гы
гы![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() АДДЮађЖдгІЯрЕШЃЌДгЖј
АДДЮађЖдгІЯрЕШЃЌДгЖј![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊМЏКЯA= ![]() ЃЎ ЃЈЂёЃЉЧѓAЁЩBЃЌЃЈRBЃЉЁШAЃЛ
ЃЎ ЃЈЂёЃЉЧѓAЁЩBЃЌЃЈRBЃЉЁШAЃЛ
ЃЈЂђЃЉШєCAЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЁао4-5ЃКВЛЕШЪНбЁНВ
вбжЊКЏЪ§![]()
ЃЈЂёЃЉЧѓВЛЕШЪН![]() ЕФНтМЏЃЛ
ЕФНтМЏЃЛ
ЃЈЂђЃЉвбжЊКЏЪ§![]() ЕФзюаЁжЕЮЊ
ЕФзюаЁжЕЮЊ![]() ЃЌШєЪЕЪ§
ЃЌШєЪЕЪ§![]() Чв
Чв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФ
ЕФ
зюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєaЁЪRЃЌдђЁАЙигкxЕФЗНГЬx2+ax+1=0ЮоЪЕИљЁБЪЧЁАz=ЃЈ2aЉ1ЃЉ+ЃЈaЉ1ЃЉiЃЈЦфжаiБэЪОащЪ§ЕЅЮЛЃЉдкИДЦНУцЩЯЖдгІЕФЕуЮЛгкЕкЫФЯѓЯоЁБЕФЃЈ ЃЉ
A.ГфЗжЗЧБивЊЬѕМў
B.БивЊЗЧГфЗжЬѕМў
C.ГфвЊЬѕМў
D.МШЗЧГфЗжгжЗЧБивЊЬѕМў
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§fЃЈxЃЉдкRЩЯПЩЕМЃЌЦфЕМКЏЪ§ЮЊfЁфЃЈxЃЉЃЌЧвКЏЪ§y=ЃЈ1ЉxЃЉfЁфЃЈxЃЉЕФЭМЯѓШчЭМЫљЪОЃЌдђЯТСаНсТлжавЛЖЈГЩСЂЕФЪЧЃЈ ЃЉ 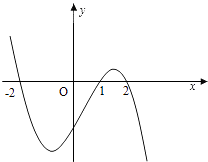
A.КЏЪ§fЃЈxЃЉгаМЋДѓжЕfЃЈ2ЃЉКЭМЋаЁжЕfЃЈ1ЃЉ
B.КЏЪ§fЃЈxЃЉгаМЋДѓжЕfЃЈЉ2ЃЉКЭМЋаЁжЕfЃЈ1ЃЉ
C.КЏЪ§fЃЈxЃЉгаМЋДѓжЕfЃЈ2ЃЉКЭМЋаЁжЕfЃЈЉ2ЃЉ
D.КЏЪ§fЃЈxЃЉгаМЋДѓжЕfЃЈЉ2ЃЉКЭМЋаЁжЕfЃЈ2ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєНЋКЏЪ§y=cos 2xЕФЭМЯѓЯђзѓЦНвЦ ![]() ИіЕЅЮЛГЄЖШЃЌдђЦНвЦКѓЭМЯѓЕФЖдГЦжсЮЊЃЈ ЃЉ
ИіЕЅЮЛГЄЖШЃЌдђЦНвЦКѓЭМЯѓЕФЖдГЦжсЮЊЃЈ ЃЉ
A.x= ![]() Љ
Љ ![]() ЃЈkЁЪZЃЉ
ЃЈkЁЪZЃЉ
B.x= ![]() +
+ ![]() ЃЈkЁЪZЃЉ
ЃЈkЁЪZЃЉ
C.x= ![]() Љ
Љ ![]() ЃЈkЁЪZЃЉ
ЃЈkЁЪZЃЉ
D.x= ![]() +
+ ![]() ЃЈkЁЪZЃЉ
ЃЈkЁЪZЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊPЪЧБпГЄЮЊ2ЕФе§Ш§НЧаЮABCБпBCЩЯЕФЖЏЕуЃЌдђ ![]() ЕФжЕЃЈ ЃЉ
ЕФжЕЃЈ ЃЉ
A.ЪЧЖЈжЕ6
B.зюДѓжЕЮЊ8
C.зюаЁжЕЮЊ2
D.гыPЕуЮЛжУгаЙи
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=xЉalnxЃЈaЁЪRЃЉ
ЃЈ1ЃЉЕБa=2ЪБЃЌЧѓЧњЯпy=fЃЈxЃЉдкЕуAЃЈ1ЃЌfЃЈ1ЃЉЃЉДІЕФЧаЯпЗНГЬЃЛ
ЃЈ2ЃЉЧѓКЏЪ§fЃЈxЃЉЕФМЋжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊaЮЊГЃЪ§ЃЌКЏЪ§fЃЈxЃЉ=xЃЈlnxЉaxЃЉгаСНИіМЋжЕЕуx1 ЃЌ x2ЃЈx1ЃМx2ЃЉЃЈ ЃЉ
A.![]()
B.![]()
C.![]()
D.![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com