已知等比数列{an}中,a2=9,S2=12.
(1)求数列{an}的通项公式;
(2)求使Sn≥2012成立的最小正整数n.
解:(1)设等比数列{a
n}的首项为a
1,公比为q,
由a
2=9,S
2=12,得:
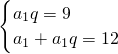
,
解得:
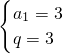
.
所以,
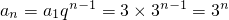
.
(2)由a
2=9,S
2=12,知等比数列的公比q≠1,
所以,
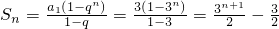
.
由S
n≥2012,得:
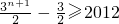
,
所以3
n+1≥4027,n≥log
34027-1.
因为log
34027-1≤log
36561-1=
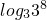
-1=7.
所以,n≥7.
则使S
n≥2012成立的最小正整数n的值为7.
分析:(1)设出等比数列的首项和公比,根据给出的条件列方程组求出首项和公比,则通项公式可求;
(2)求出等比数列的前n项和,代入不等式S
n≥2012,化指数式为对数式后可求n的最小值.
点评:本题考查了等比数列的通项公式,等比数列的前n项和,考查了含参数的不等式恒成立问题,在求解该题的过程中,求解n的范围是学生易出错的地方,此题是中档题.

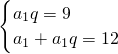 ,
,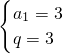 .
.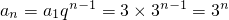 .
.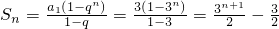 .
.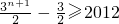 ,
,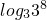 -1=7.
-1=7.
