
长为3的线段两端点A,B分别在x轴正半轴和y轴的正半轴上滑动, ,点P的轨迹为曲线C.
,点P的轨迹为曲线C.
(1)以直线AB的倾斜角 为参数,求曲线C的参数方程;
为参数,求曲线C的参数方程;
(2)求点P到点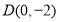 距离的最大值.
距离的最大值.
(1)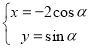 (α为参数,90?<α<180?);(2)
(α为参数,90?<α<180?);(2)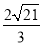 .
.
【解析】
试题分析:本题主要考查参数方程、两点间距离公式、直角三角形中的正弦、余弦值的计算、平方关系、配方法、三角函数的有界性等基础知识,考查学生的分析问题解决问题的能力、数形结合的能力、计算能力.第一问,设出点P的坐标,在三角形AOB中,利用正弦公式、余弦公式计算x,y的值,得到曲线C的参数方程,注意角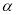 的取值范围;第二问,利用第一问求出的点P坐标的x,y值,用两点间距离公式得到表达式,利用平方关系、配方法、三角函数的有界性求表达式的最值.
的取值范围;第二问,利用第一问求出的点P坐标的x,y值,用两点间距离公式得到表达式,利用平方关系、配方法、三角函数的有界性求表达式的最值.
试题解析:(1)设P(x,y),由题设可知,
则x=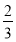 |AB|cos(?-α)=-2cosα,y=
|AB|cos(?-α)=-2cosα,y= |AB|sin(?-α)=sinα,
|AB|sin(?-α)=sinα,
所以曲线C的参数方程为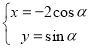 (α为参数,90?<α<180?). 5分
(α为参数,90?<α<180?). 5分
(2)由(1)得
|PD|2=(-2cosα)2+(sinα+2)2=4cos2α+sin2α+4sinα+4
=-3sin2α+4sinα+8=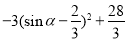 .
.
当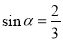 时,|PD|取最大值
时,|PD|取最大值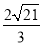 . 10分
. 10分
考点:参数方程、两点间距离公式、直角三角形中的正弦、配方法、三角函数的有界性.


科目:高中数学 来源:2013-2014学年河北省高三第一次模拟考试文科数学试卷(解析版) 题型:解答题
已知函数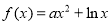 (
(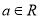 )
)
(1)当a=2时,求 在区间[e,e2]上的最大值和最小值;
在区间[e,e2]上的最大值和最小值;
(2)如果函数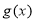 、
、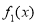 、
、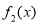 在公共定义域D上,满足
在公共定义域D上,满足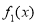 <
<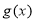 <
<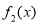 ,那么就称
,那么就称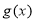 为
为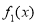 、
、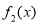 的“伴随函数”.已知函数
的“伴随函数”.已知函数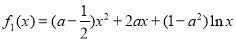 ,
,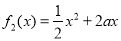 ,若在区间(1,+∞)上,函数
,若在区间(1,+∞)上,函数 是
是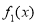 、
、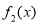 的“伴随函数”,求a的取值范围。
的“伴随函数”,求a的取值范围。
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省石家庄市毕业班第一次模拟考试数学理科数学试卷(解析版) 题型:选择题
登山族为了了解某山高y(km)与气温x(°C)之间的关系,随机统计了4次山高与相应的气温,并制作了对照表:
气温x(°C) | 18 | 13 | 10 | -1 |
山高y(km) | 24 | 34 | 38 | 64 |
由表中数据,得到线性回归方程 ,由此请估计出山高为72(km)处气温的度数为( )
,由此请估计出山高为72(km)处气温的度数为( )
A.-10 B.-8 C.-6 D.-6
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省石家庄市毕业班第一次模拟考试数学理文数学试卷(解析版) 题型:选择题
已知f(x)是定义在R上的以3为周期的偶函数,若f(1)<1,f(5)= ,则实数a的取值范围为()
,则实数a的取值范围为()
A.-1<a<4 B.-2<a<1 C.-1<a<2 D.-1<a<0
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省石家庄市毕业班第一次模拟考试数学理文数学试卷(解析版) 题型:选择题
已知a=3 ,b=log
,b=log ,c=log
,c=log ,则()
,则()
A.a>b>cB.b>c>aC.b>a>cD.c>b>a
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省唐山市高三年级第二次模拟考试理科数学试卷(解析版) 题型:解答题
甲向靶子A射击两次,乙向靶子射击一次.甲每次射击命中靶子的概率为0.8,命中得5分;乙命中靶子的概率为0.5,命中得10分.
(1)求甲、乙二人共命中一次目标的概率;
(2)设X为二人得分之和,求X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省唐山市高三年级第二次模拟考试理科数学试卷(解析版) 题型:选择题
已知椭圆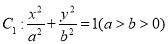 与圆
与圆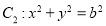 ,若在椭圆
,若在椭圆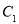 上存在点P,使得由点P所作的圆
上存在点P,使得由点P所作的圆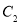 的两条切线互相垂直,则椭圆
的两条切线互相垂直,则椭圆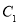 的离心率的取值范围是( )
的离心率的取值范围是( )
A. B.
B.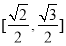 C.
C.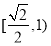 D.
D.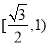
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省唐山市高三年级第二次模拟考试文科数学试卷(解析版) 题型:解答题
某种水果的单个质量在500g以上视为特等品.随机抽取1000个该水果,结果有50个特等品.将这50个水果的质量数据分组,得到下边的频率分布表.
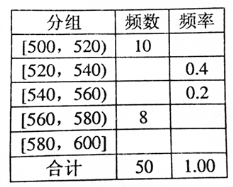
(1)估计该水果的质量不少于560g的概率;
(2)若在某批水果的检测中,发现有15个特等品,据此估计该批水果中没有达到特等品的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com