
分析 取AC,BC的中点分别为E,F;化简可得2$\overrightarrow{OE}$+4$\overrightarrow{OF}$=0,从而记|$\overrightarrow{OF}$|=x,则|$\overrightarrow{OE}$|=2x,|AB|=6x,|AC|=|EC|=$\frac{2x}{cosA}$,|EH|=2xcosA,从而可得$\frac{2xcosA+\frac{2x}{cosA}}{6x}$=cosA,从而解得.
解答 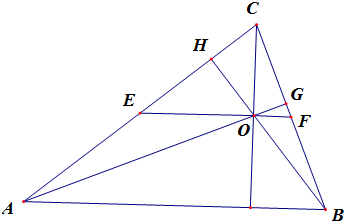 解:∵$\overrightarrow{OA}$+2$\overrightarrow{OB}$+3$\overrightarrow{OC}$=$\overrightarrow{0}$,
解:∵$\overrightarrow{OA}$+2$\overrightarrow{OB}$+3$\overrightarrow{OC}$=$\overrightarrow{0}$,
∴$\overrightarrow{OA}$+$\overrightarrow{OC}$+2$\overrightarrow{OB}$+2$\overrightarrow{OC}$=$\overrightarrow{0}$,
取AC,BC的中点分别为E,F;
∴2$\overrightarrow{OE}$+4$\overrightarrow{OF}$=0,
记|$\overrightarrow{OF}$|=x,则|$\overrightarrow{OE}$|=2x,
|AB|=6x,|AE|=|EC|=$\frac{2x}{cosA}$,|EH|=2xcosA,
故$\frac{2xcosA+\frac{2x}{cosA}}{6x}$=cosA,
即$\frac{1}{cosA}$=2cosA,
解得cosA=$\frac{\sqrt{2}}{2}$或cosA=-$\frac{\sqrt{2}}{2}$(舍去),
故A=$\frac{π}{4}$,
故答案为:$\frac{π}{4}$.
点评 本题考查了平面向量的化简运算及解三角形的应用,同时考查了数形结合的思想方法应用.


科目:高中数学 来源: 题型:解答题
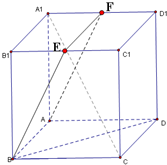 在单位正方体ABCD-A1B1C1D1中,E,F分别是B1C1,A1D1的中点.
在单位正方体ABCD-A1B1C1D1中,E,F分别是B1C1,A1D1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=1 | B. | x=2 | C. | x=-1或x=1 | D. | x=-2或x=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 我国人口老龄化日渐突出,2016年初,“二孩”政策全面实施,根据国家统计,在2015年初,中国大陆人口总数约13.7亿,人口出生率约为12‰,人口死亡率约为7‰,人口增长率约为5‰,其中人口年龄比例如下表:
我国人口老龄化日渐突出,2016年初,“二孩”政策全面实施,根据国家统计,在2015年初,中国大陆人口总数约13.7亿,人口出生率约为12‰,人口死亡率约为7‰,人口增长率约为5‰,其中人口年龄比例如下表:| 年龄段 | 16周岁以下 | 17至59周岁(劳动年龄) | 60周岁及以上 |
| 68% | 16% |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 标准差 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com