
【题目】已知函数f(x)=4tanxsin( ![]() ﹣x)cos(x﹣
﹣x)cos(x﹣ ![]() )﹣
)﹣ ![]() .
.
(1)求f(x)的定义域与最小正周期;
(2)讨论f(x)在区间[﹣ ![]() ,
, ![]() ]上的单调性.
]上的单调性.
【答案】
(1)解:∵f(x)=4tanxsin( ![]() ﹣x)cos(x﹣
﹣x)cos(x﹣ ![]() )﹣
)﹣ ![]() .
.
∴x≠kπ+ ![]() ,即函数的定义域为{x|x≠kπ+
,即函数的定义域为{x|x≠kπ+ ![]() ,k∈Z},
,k∈Z},
则f(x)=4tanxcosx( ![]() cosx+
cosx+ ![]() sinx)﹣
sinx)﹣ ![]()
=4sinx( ![]() cosx+
cosx+ ![]() sinx)﹣
sinx)﹣ ![]()
=2sinxcosx+2 ![]() sin2x﹣
sin2x﹣ ![]()
=sin2x+ ![]() (1﹣cos2x)﹣
(1﹣cos2x)﹣ ![]()
=sin2x﹣ ![]() cos2x
cos2x
=2sin(2x﹣ ![]() ),
),
则函数的周期T= ![]()
(2)解:由2kπ﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,
,k∈Z,
得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,即函数的增区间为[kπ﹣
,k∈Z,即函数的增区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z,
],k∈Z,
当k=0时,增区间为[﹣ ![]() ,
, ![]() ],k∈Z,
],k∈Z,
∵x∈[﹣ ![]() ,
, ![]() ],∴此时x∈[﹣
],∴此时x∈[﹣ ![]() ,
, ![]() ],
],
由2kπ+ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,
,k∈Z,
得kπ+ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,即函数的减区间为[kπ+
,k∈Z,即函数的减区间为[kπ+ ![]() ,kπ+
,kπ+ ![]() ],k∈Z,
],k∈Z,
当k=﹣1时,减区间为[﹣ ![]() ,﹣
,﹣ ![]() ],k∈Z,
],k∈Z,
∵x∈[﹣ ![]() ,
, ![]() ],∴此时x∈[﹣
],∴此时x∈[﹣ ![]() ,﹣
,﹣ ![]() ],
],
即在区间[﹣ ![]() ,
, ![]() ]上,函数的减区间为∈[﹣
]上,函数的减区间为∈[﹣ ![]() ,﹣
,﹣ ![]() ],增区间为[﹣
],增区间为[﹣ ![]() ,
, ![]() ].
].
【解析】(1)利用三角函数的诱导公式以及两角和差的余弦公式,结合三角函数的辅助角公式进行化简求解即可.(2)利用三角函数的单调性进行求解即可.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,AB∥CD,∠ADC=90°,PD=AD=AB=1,DC=2. 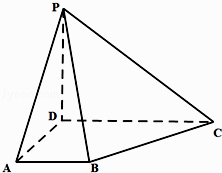
(1)求证:BC⊥平面PBD;
(2)求二面角A﹣PB﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,F1、F2是双曲线 ![]() =1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点A、B.若△ABF2为等边三角形,则双曲线的离心率为( )
=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点A、B.若△ABF2为等边三角形,则双曲线的离心率为( ) 
A.4
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°. 
(1)求证:PC⊥BC;
(2)求点A到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1、F2是椭圆 ![]() +
+ ![]() =1的左、右焦点,O为坐标原点,点P(﹣1,
=1的左、右焦点,O为坐标原点,点P(﹣1, ![]() )在椭圆上,线段PF2与y轴的交点M满足
)在椭圆上,线段PF2与y轴的交点M满足 ![]() +
+ ![]() =
= ![]() ;
;
(1)求椭圆的标准方程;
(2)⊙O是以F1F2为直径的圆,一直线l:y=kx+m与⊙O相切,并与椭圆交于不同的两点A、B.当 ![]() =λ且满足
=λ且满足 ![]() ≤λ≤
≤λ≤ ![]() 时,求△AOB面积S的取值范围.
时,求△AOB面积S的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|x2+2x﹣3<0},集合B={x||x+a|<1}.
(1)若a=3,求A∪B;
(2)设命题p:x∈A,命题q:x∈B,若p是q成立的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的方程为:ax2+ay2﹣2a2x﹣4y=0(a≠0,a为常数).
(1)判断曲线C的形状;
(2)设曲线C分别与x轴、y轴交于点A、B(A、B不同于原点O),试判断△AOB的面积S是否为定值?并证明你的判断;
(3)设直线l:y=﹣2x+4与曲线C交于不同的两点M、N,且|OM|=|ON|,求曲线C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面区域  恰好被面积最小的圆C:(x﹣a)2+(y﹣b)2=r2及其内部所覆盖.
恰好被面积最小的圆C:(x﹣a)2+(y﹣b)2=r2及其内部所覆盖.
(1)试求圆C的方程.
(2)若斜率为1的直线l与圆C交于不同两点A,B满足CA⊥CB,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com