
分析 先求出双曲线x2-y2=4的左顶点为A(-4,0),根据双曲线的对称性,设出B(x1,y1),C(x1,-y1)的坐标,根据,△ABC是等边三角形得(x1+2)2+y12=(-y1-y1)2,求出x1和y1的值,由此得BC=4$\sqrt{3}$,从而可以算出面积.
解答 解:双曲线x2-y2=4的左顶点为A(-2,0),根据双曲线的对称性,
可设B(x1,y1),C(x1,-y1).
由△ABC是等边三角形⇒AB=BC,得:
(x1+2)2+y12=(-y1-y1)2,
又x12-y12=4,
∴x12-2x1-8=0,∴x1=-2或x1=4
右支的范围是x≥0,
所以x1=4,从而y1=±2$\sqrt{3}$,
由此BC=4$\sqrt{3}$
可以算出面积:S=$\frac{\sqrt{3}}{4}×(4\sqrt{3})^{2}$=12$\sqrt{3}$.
故答案为:12$\sqrt{3}$.
点评 本小题主要考查双曲线的标准方程、双曲线的简单性质等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
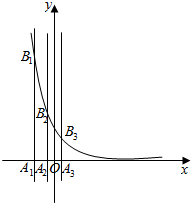 (文)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=($\frac{1}{2}$)x的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.
(文)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=($\frac{1}{2}$)x的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
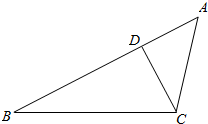 如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.
如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若d1-d2=0,则直线P1P2与直线l平行 | |
| B. | 若d1+d2=0,则直线P1P2与直线l平行 | |
| C. | 若d1+d2=0,则直线P1P2与直线l垂直 | |
| D. | 若d1•d2<0,则直线P1P2与直线l相交 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com