练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    均值为2，方差为2π的正态分布的概率密度函数为________．

     

    f(x)＝

    【解析】在密度函数f(x)＝中，

    μ＝2，σ＝，故f(x)＝.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015届辽宁省大连市五校高二下学期期末考试文科数学试卷（解析版） 题型：解答题

    某县为增强市民的环境保护意识，面向全县征召义务宣传志愿者，先从符合条件的志愿者中随机抽取100名按年龄分组：第1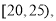组第2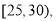组第3组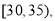第4组第5组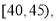得到的频率分布直方图如图所示,

    （1）分别求第3，4，5组的频率。

    （2）若从第3，4，5组中用分层抽样的方法抽取6名志愿者参与广场的宣传活动，应从第3,4,5组各抽取多少名志愿者.

    （3）在（2）的条件下，该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验，求第4组至少有一名志愿者被抽中的概率.

     

     

    查看答案和解析>>

    科目：高中数学 来源：2015届贵州省高二下学期期中文科数学试卷（解析版） 题型：解答题

    某种产品的广告费用支出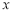（万元）与销售额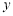（万元）之间有如下的对应数据：

    2

    4

    5

    6

    8

    30

    40

    60

    50

    70

    x

    2

    4

    5

    6

    8

    y

    30

    40

    60

    50

    70

     

    （1）画出散点图；

    （2）求回归直线方程；

    （3）据此估计广告费用为9万元时，销售收入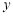的值．

    参考公式：回归直线的方程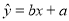，其中

    ．

     

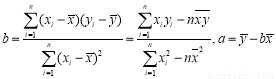    查看答案和解析>>

    科目：高中数学 来源：2015届贵州省高二下学期期中文科数学试卷（解析版） 题型：选择题

    若抛物线的焦点与椭圆的左焦点重合，则的值为（ ）

    A．－8 B．－16 C． D．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标模块练习卷（解析版） 题型：解答题

    某市公租房房屋位于A、B、C三个地区，设每位申请人只申请其中一个片区的房屋，且申请其中任一个片区的房屋是等可能的，求该市的任4位申请人中：

    (1)若有2人申请A片区房屋的概率；

    (2)申请的房屋在片区的个数的X分布列与期望．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标模块练习卷（解析版） 题型：填空题

    直线方程Ax＋By＝0，若从1,2,3,6,7,8这六个数字中每次取两个不同的数作为A、B的值，则表示不同直线的条数是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标3章练习卷（解析版） 题型：解答题

    在电阻碳含量对于电阻的效应研究中，得到如下表所示的数据：

    含碳量

    (x/%)

    0.10

    0.30

    0.40

    0.55

    0.70

    0.80

    0.95

    20 ℃时电阻

    (y/Ω)

    15

    18

    19

    21

    22.6

    23.8

    26

    (1)求出y与x的相关系数并判断相关性；

    (2)求出电阻y关于含碳量x之间的回归直线方程．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标3.2练习卷（解析版） 题型：解答题

    一个车间为了规定工时定额．需要确定加工零件所花费的时间，为此进行了10次试验．测得的数据如下：

    零件数x/个

    10

    20

    30

    40

    50

    60

    70

    80

    90

    100

    加工时间y/分

    62

    68

    75

    81

    89

    95

    102

    108

    115

    122

    (1)y与x是否具有线性相关关系？

    (2)如果y与x具有线性相关关系，求回归直线方程；

    (3)根据求出的回归直线方程，预测加工200个零件所用的时间为多少？

     

    查看答案和解析>>

    科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标2.6练习卷（解析版） 题型：填空题

    如图是当σ取三个不同值σ1、σ2、σ3时的三种正态曲线N(0，σ2)的图象，那么σ1、σ2、σ3的大小关系是________．

     

     

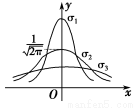
    查看答案和解析>>

    同步练习册答案