
一个车间为了规定工时定额.需要确定加工零件所花费的时间,为此进行了10次试验.测得的数据如下:
零件数x/个 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
加工时间y/分 | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
(1)y与x是否具有线性相关关系?
(2)如果y与x具有线性相关关系,求回归直线方程;
(3)根据求出的回归直线方程,预测加工200个零件所用的时间为多少?
(1)x与y之间有很强的线性相关关系,因而可求回归直线方程
(2)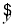 =0.668x+54.96
=0.668x+54.96
(3)189分
【解析】
解:(1)列出下表:
i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
xi | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
yi | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
xiyi | 620 | 1 360 | 2 250 | 3 240 | 4 450 | 5 700 | 7 140 | 8 640 | 10 350 | 12 200 |
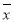 =55,
=55,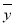 =91.7,
=91.7,
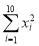 =38 500,
=38 500,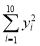 =87 777,
=87 777,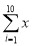 iyi=55 950,
iyi=55 950,
因此r=
=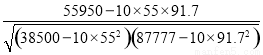 ≈0.999 8.
≈0.999 8.
由于r=0.999 8>0.75,因此x与y之间有很强的线性相关关系,因而可求回归直线方程.
(2)设所求的回归直线方程为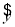 =
=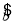 x+
x+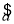 ,则有
,则有
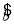 =
= =
=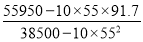 ≈0.668,
≈0.668,
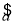 =
=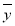 -
-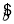
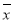 =91.7-0.668×55=54.96,
=91.7-0.668×55=54.96,
因此,所求的回归直线方程为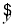 =0.668x+54.96.
=0.668x+54.96.
(3)这个回归直线方程的意义是当x每增大1时,y的值约增加0.668,而54.96是y不随x增加而变化的部分.因此,当x=200时,y的估计值为=0.668×200+54.96=188.56≈189.
因此,加工200个零件所用的工时约为189分.


科目:高中数学 来源:2015届贵州省高二下学期期中理科数学试卷(解析版) 题型:选择题
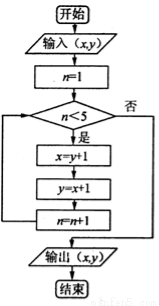
已知某算法的流程图如图所示,输入的数x和y为自然数,若已知输出的有序数对为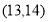 ,则开始输入的有序数对
,则开始输入的有序数对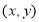 可能为( )
可能为( )
A.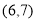 B.
B.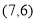 C.
C.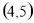 D.
D.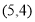
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标3章练习卷(解析版) 题型:填空题
对有关数据的分析可知,每一立方米混凝土的水泥用量x(单位:kg)与28天后混凝土的抗压度y(单位:kg/cm2)之间具有线性相关关系,其线性回归方程为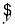 =0.30x+9.99.根据建设项目的需要,28天后混凝土的抗压度不得低于89.7 kg/cm2,每立方米混凝土的水泥用量最少应为________kg.(精确到0.1 kg)
=0.30x+9.99.根据建设项目的需要,28天后混凝土的抗压度不得低于89.7 kg/cm2,每立方米混凝土的水泥用量最少应为________kg.(精确到0.1 kg)
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标3章练习卷(解析版) 题型:填空题
已知x,Y之间的数据如下表所示,则Y与x之间的线性回归直线一定过点________.
x | 1.08 | 1.12 | 1.19 | 1.28 |
Y | 2.25 | 2.37 | 2.40 | 2.55 |
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标3.2练习卷(解析版) 题型:填空题
以下关于线性回归的判断,正确的是________.
①散点图中所有点都在一条直线附近,这条直线为回归直线
②散点图中的绝大多数点都在回归直线的附近,个别特殊点不影响线性回归性
③已知直线方程为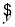 =0.50x-0.81,则x=25时,
=0.50x-0.81,则x=25时,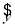 为11.69
为11.69
④回归直线方程的意义是它反映了样本整体的变化趋势
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标3.1练习卷(解析版) 题型:解答题
有甲、乙两个工厂生产同一种产品,产品分为一等品和二等品.为了考察这两个工厂的产品质量的水平是否一致,从甲、乙两个工厂中分别随机地抽出产品109件,191件,其中甲工厂一等品58件,二等品51件,乙工厂一等品70件,二等品121件.
(1)根据以上数据,建立2×2列联表;
(2)试分析甲、乙两个工厂的产品质量有无显著差别(可靠性不低于99%).
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2章练习卷(解析版) 题型:填空题
马老师从课本上抄录一个随机变量X的概率分布律如下表
x | 1 | 2 | 3 |
P(ε=x) | ? | ! | ? |
请小牛同学计算ε的数学期望,尽管“!”处无法完全看清,且两个“?”处字迹模糊,但能肯定这两个“?”处的数值相同.据此,小牛给出了正确答案E(ε)=________.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.5练习卷(解析版) 题型:填空题
若随机变量X~B(n,0.6),且E(X)=3,则P(X=1)的值是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com