
【题目】如图,在矩形ABCD中,AB=8,BC=4,E为DC边的中点,沿AE将△ADE折起,在折起过程中,有几个正确( )

①ED⊥平面ACD ②CD⊥平面BED
③BD⊥平面ACD ④AD⊥平面BED
A.1个B.2个C.3个D.4个
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)当![]() 时,函数
时,函数![]() 有两个极值点,求
有两个极值点,求![]() 的取值范围;
的取值范围;
(2)若![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行,且函数
轴平行,且函数![]() 在
在![]() 时,其图象上每一点处切线的倾斜角均为锐角,求
时,其图象上每一点处切线的倾斜角均为锐角,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
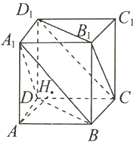
【题目】如图,正方体![]() 的棱长为1,过
的棱长为1,过![]() 点作平面
点作平面![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,有下面三个结论:①点
,有下面三个结论:①点![]() 是
是![]() 的中心;②
的中心;②![]() 垂直于平面
垂直于平面![]() ;③直线
;③直线![]() 与直线
与直线![]() 所成的角是90°.其中正确结论的序号是_______.
所成的角是90°.其中正确结论的序号是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次商品的有奖销售活动中,有![]() 人获三等奖.三等奖的奖品共有四种,每个三等奖获得者随意从四种奖品中挑选一种,结果有一种奖品无人挑选的概率是______.
人获三等奖.三等奖的奖品共有四种,每个三等奖获得者随意从四种奖品中挑选一种,结果有一种奖品无人挑选的概率是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com