
【题目】设函数![]() ,
,![]() .
.
(1)当![]() 时,函数
时,函数![]() 有两个极值点,求
有两个极值点,求![]() 的取值范围;
的取值范围;
(2)若![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行,且函数
轴平行,且函数![]() 在
在![]() 时,其图象上每一点处切线的倾斜角均为锐角,求
时,其图象上每一点处切线的倾斜角均为锐角,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)求得导函数![]() ,题意说明
,题意说明![]() 有两个零点,即
有两个零点,即![]() 有两个解,或直线
有两个解,或直线![]() 与函数
与函数![]() 的有两个交点,可用导数研究
的有两个交点,可用导数研究![]() 的性质(单调性,极值等),由零点存在定理即可得
的性质(单调性,极值等),由零点存在定理即可得![]() 的范围;
的范围;
(2)首先题意说明![]() ,
,![]() ,从而有
,从而有![]() 且
且![]() ,其次
,其次![]() 时,
时,![]() 恒成立,因此
恒成立,因此![]() 的最小值大于0,这可由导数来研究,从而得出
的最小值大于0,这可由导数来研究,从而得出![]() 的范围.
的范围.
(1)当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 有两个极值点就是方程
有两个极值点就是方程![]() 有两个解,
有两个解,
令![]() ,则
,则![]() .
.
当![]() 时,
时,![]() 在区间
在区间![]() 上恒成立,则
上恒成立,则![]() 此时单调递增,
此时单调递增,
又![]() 为连续函数,由零点存在定理可知:
为连续函数,由零点存在定理可知:
![]() 最多只有一个零点,也即
最多只有一个零点,也即![]() 最多只有一个解,不符合题意;
最多只有一个解,不符合题意;
当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,
故![]() 在区间
在区间![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
![]() ,
,
若![]() ,即
,即![]() 时,根据函数单调性可知:
时,根据函数单调性可知:
此时![]() ,故
,故![]() 无解,不符合题意;
无解,不符合题意;
若![]() ,即
,即![]() 时,根据函数单调性可知:
时,根据函数单调性可知:
此时![]() ,只有一个解,不符合题意;
,只有一个解,不符合题意;
若![]() ,即
,即![]() 时,
时,
又![]() ,
,![]() ,(最后进行证明)
,(最后进行证明)
又![]() ,故由零点存在定理可知:
,故由零点存在定理可知:
![]() 此时有两个根,满足题意.
此时有两个根,满足题意.
综上![]() .
.
现证:![]() ,
,
令![]() ,故
,故![]() ,
,
故![]() 在定义域内单调递增,
在定义域内单调递增,
故![]() ,
,
即证![]() .
.
(2)函数![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行,
轴平行,
所以![]() 且
且![]() ,因为
,因为![]() ,
,
所以![]() 且
且![]() ;
;
![]() 在
在![]() 时,
时,
其图象的每一点处的切线的倾斜角均为锐角,
即当![]() 时,
时,![]() 恒成立,即
恒成立,即
![]() ,
,
令![]() ,∴
,∴![]()
设![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 单调递增,即
单调递增,即![]() 在
在![]() 单调递增,
单调递增,
∴![]() ,
,
当![]() 且
且![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 单调递增;
单调递增;
∴![]() 成立
成立
当![]() ,因为
,因为![]() 在
在![]() 单调递增,
单调递增,
所以![]() ,
,
![]() ,
,
所以存在![]() 有
有![]() ;
;
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
所以有![]() ,
,![]() 不恒成立;
不恒成立;
所以实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】在单位正![]() 内任取一点P,以PA、PB、PC为边生成
内任取一点P,以PA、PB、PC为边生成![]() .
.
(1)当![]() 分别为锐角三角形、直角三角形、钝角三角形时,求出点P的轨迹.
分别为锐角三角形、直角三角形、钝角三角形时,求出点P的轨迹.
(2)证明:当![]() 的周长取最小值时,面积取最大值.
的周长取最小值时,面积取最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的个数是( )
①由五个面围成的多面体只能是三棱柱;
②由若干个平面多边形所围成的几何体是多面体;
③仅有一组对面平行的五面体是棱台;
④有一面是多边形,其余各面是三角形的几何体是棱锥.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三国时代数学家赵爽在《周髀算经》中利用弦图,给出了勾股定理的绝妙证明.图中包含四个全等的直角三角形及一个小正方形(阴影),设直角三角形有一内角为![]() ,若向弦图内随机抛掷500颗米粒(大小忽略不计,取
,若向弦图内随机抛掷500颗米粒(大小忽略不计,取![]() ),则落在小正方形(阴影)内的米粒数大约为( )
),则落在小正方形(阴影)内的米粒数大约为( )
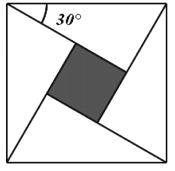
A. 134 B. 67 C. 200 D. 250
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆台的上、下底面半径分别为5cm,10cm,母线长![]() ,从圆台母线
,从圆台母线![]() 的中点
的中点![]() 拉一条绳子绕圆台侧面转到
拉一条绳子绕圆台侧面转到![]() 点.求:
点.求:

(1)绳子的最短长度;
(2)在绳子最短时,求上底面圆周上的点到绳子的最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了对某课题进行研究,分别从A,B,C三所高校中用分层随机抽样法抽取若干名教授组成研究小组,其中高校A有m名教授,高校B有72名教授,高校C有n名教授(其中![]() )
)
(1)若A,B两所高校中共抽取3名教授,B,C两所高校中共抽取5名教授,求m,n;
(2)若高校B中抽取的教授数是高校A和C中抽取的教授总数的![]() ,求三所高校的教授的总人数.
,求三所高校的教授的总人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=4,E为DC边的中点,沿AE将△ADE折起,在折起过程中,有几个正确( )

①ED⊥平面ACD ②CD⊥平面BED
③BD⊥平面ACD ④AD⊥平面BED
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面边长为![]() 、高为
、高为![]() 的正六棱柱
的正六棱柱![]() 展厅内,长为
展厅内,长为![]() ,宽为
,宽为![]() 的矩形油画
的矩形油画![]() 挂在厅内正前方中间.
挂在厅内正前方中间.
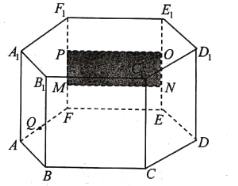
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当游客![]() 在
在![]() 上看油画的纵向视角(即
上看油画的纵向视角(即![]() )最大时,求
)最大时,求![]() 与油画平面所成的角.
与油画平面所成的角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com