
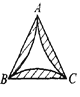
【题目】在单位正![]() 内任取一点P,以PA、PB、PC为边生成
内任取一点P,以PA、PB、PC为边生成![]() .
.
(1)当![]() 分别为锐角三角形、直角三角形、钝角三角形时,求出点P的轨迹.
分别为锐角三角形、直角三角形、钝角三角形时,求出点P的轨迹.
(2)证明:当![]() 的周长取最小值时,面积取最大值.
的周长取最小值时,面积取最大值.
【答案】(1)见解析;(2)![]()
【解析】
如图,记![]() .
.
将![]() 绕点B逆时针旋转
绕点B逆时针旋转![]() 得
得![]() ,则
,则![]() ,
,![]() .
.![]() 就是由PA、PB、PC所组成的
就是由PA、PB、PC所组成的![]() ,且其三个内角
,且其三个内角![]() ,
,![]() ,
,![]() .
.

(1)当存在![]() 时,
时,![]() 为直角三角形.
为直角三角形.
由![]() ,知
,知![]() .
.
所以,点P在三个单位圆的![]() 弧AB、BC、CA上(图).
弧AB、BC、CA上(图).
当存在![]() 时,
时,![]() 为钝角三角形.
为钝角三角形.
由![]() ,知
,知![]() .
.
由圆内角大于圆周角知,点P在图中的三个弓形内(阴影部分,不包括边界).
当![]() ,
,![]() ,
,![]() 同时成立时,
同时成立时,![]() 为锐角三角形,得
为锐角三角形,得![]() ,
,![]() ,
,![]() .
.
由圆外角小于圆周角知,点P在图8中的三个圆弧外(曲边![]() 内部,不包括边界).
内部,不包括边界).
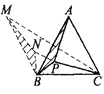
(2)先确定![]() 周长取最小值时点P的位置.为此,将如图的
周长取最小值时点P的位置.为此,将如图的![]() 绕点B逆时针旋转
绕点B逆时针旋转![]() 得
得![]() ,联结MC、PN.则折线
,联结MC、PN.则折线![]() .
.
当且仅当M、N、P、C四点共线时,![]() 的周长取最小值.此时,有
的周长取最小值.此时,有![]() ,即点P为
,即点P为![]() 的中心(
的中心(![]() ).
).
下面说明,这恰好是面积取最大值的条件.
在![]() 中,由余弦定理和基本不等式有
中,由余弦定理和基本不等式有![]() ,
,
故![]() .当且仅当
.当且仅当![]() 时,等号成立.
时,等号成立.
在![]() 中,
中,![]() .
.
由面积公式有![]()
![]()

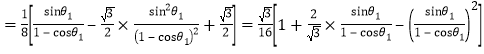
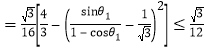 .
.
两处放大的地方同时取等号当且仅当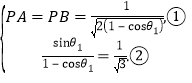
由式②有![]() .
.
所以,![]() .
.
从而,![]() ,代入式①得
,代入式①得![]() .
.
这表明,PA、PB在![]() 的中线上,且相交于距顶点
的中线上,且相交于距顶点![]() 处,点P为中心.
处,点P为中心.
所以,当点P为![]() 的中心时,
的中心时,![]() 的周长最短且面积最大,最大值为
的周长最短且面积最大,最大值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() ),且
),且![]() 的解集为
的解集为![]() ;数列
;数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意
,对任意![]() ,满足
,满足![]() .
.
(1)求![]() 的值及数列
的值及数列![]() 的通项公式;
的通项公式;
(2)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)已知数列![]() 满足
满足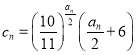 ,若
,若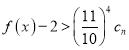 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋内装有大小相同的7个白球和1个黑球.
(1)从口袋内取出3个球,共有多少种取法?
(2)从口袋内取出3个球,使其中含有1个黑球,有多少种取法?
(3)从口袋内取出3个球,使其中不含黑球,有多少种取法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线
轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() .若直
.若直![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区为了了解青少年的身体素质,对本社区的![]() 名青少年进行了调研,随机抽取了若干名,年龄全部介于
名青少年进行了调研,随机抽取了若干名,年龄全部介于![]() 与
与![]() 岁之间,将年龄按如下方式分成五组:第一组
岁之间,将年龄按如下方式分成五组:第一组![]() ;第二组
;第二组![]() ;
;![]() ;第五组
;第五组![]() .按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三个组的频率之比为
.按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三个组的频率之比为![]() ,且第二组的频数为
,且第二组的频数为![]() .
.
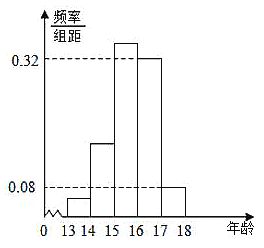
(1)试估计这![]() 名青少年中年龄在
名青少年中年龄在![]() 内的人数;
内的人数;
(2)求从本社区的![]() 名青少年中随机抽取出的调研人数.
名青少年中随机抽取出的调研人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小型企业甲产品生产的投入成本x(单位:万元)与产品销售收入y(单位:万元)存在较好的线性关系,下表记录了最近5次该产品的相关数据.
x(万元) | 3 | 5 | 7 | 9 | 11 |
y(万元) | 8 | 10 | 13 | 17 | 22 |
(1)求y关于x的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本12万元的毛利率更大还是投入成本15万元的毛利率更大(毛利率![]()
![]()
![]() )?
)?
相关公式: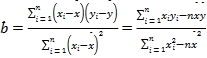 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是
A. 三棱锥的四个面可以都是直角三角形;
B. 等差数列{an}的前n项和为Sn(n=1,2,3…),若当首项a1和公差d变化时,a5+a8+a11是一个定值,则S16为定值;
C. ![]() 中,sinA>sinB是
中,sinA>sinB是![]() 的充要条件;
的充要条件;
D. 若双曲线的渐近线互相垂直,则这条双曲线是等轴双曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)当![]() 时,函数
时,函数![]() 有两个极值点,求
有两个极值点,求![]() 的取值范围;
的取值范围;
(2)若![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行,且函数
轴平行,且函数![]() 在
在![]() 时,其图象上每一点处切线的倾斜角均为锐角,求
时,其图象上每一点处切线的倾斜角均为锐角,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com