【题目】为了适应新高考改革，某校组织了一次新高考质量测评（总分100分），在成绩统计分析中，抽取12名学生的成绩以茎叶图形式表示如图，学校规定测试成绩低于87分的为“未达标”，分数不低于87分的为“达标”.
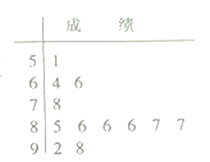
（1）求这组数据的众数和平均数；
（2）在这12名学生中从测试成绩介于80~90之间的学生中任选2人，求至少有1人“达标”的概率.
【答案】（1）86,80.5；（2）
.
【解析】
（1）找出茎叶图中出现次数最多的数为众数，根据平均数公式，即可求得平均数；
（2）在被抽取的学生中，有2个“达标”学生，4个“未达标”学生，按达标和不达标两类编号，列出从6人中任取2人的所有情况，统计出满足条件的基本事件的个数，根据古典概型的概率公式，即可求解.
(1)这组数据的众数为86；
平均数为
.
(2)在被抽取的学生中，有2个“达标”学生，4个“未达标”学生，
将“达标”学生编号为
，
，“未达标”学生编号为
，
，
，
，
则从6人中任取2人,有以下情况：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
.共15种.
其中符合条件的为，，，，，，
，，，共9种.
故至少有1人“达标”的概率
.
科目：高中数学 来源： 题型：
【题目】某城市在进行创建文明城市的活动中，为了解居民对“创文”的满意程度，组织居民给活动打分（分数为整数．满分为100分）．从中随机抽取一个容量为120的样本．发现所有数据均在
内．现将这些分数分成以下6组并画出了样本的频率分布直方图，但不小心污损了部分图形，如图所示．观察图形，回答下列问题：
（1）算出第三组
的频数．并补全频率分布直方图；
（2）请根据频率分布直方图，估计样本的众数、中位数和平均数．（每组数据以区间的中点值为代表）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50,60)，[60,70)，[70,80)，[80,90)，[90,100]．
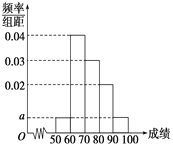
(1)求图中a的值；
(2)根据频率分布直方图，估计这100名学生语文成绩的平均分；
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示，求数学成绩在[50,90)之外的人数.
分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
x∶y | 1∶1 | 2∶1 | 3∶4 | 4∶5 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】将红、黑、蓝、白5张纸牌（其中白纸牌有2张）随机分发给甲、乙、丙、丁4个人，每人至少分得1张，则下列两个事件为互斥事件的是（ ）
A. 事件“甲分得1张白牌”与事件“乙分得1张红牌”
B. 事件“甲分得1张红牌”与事件“乙分得1张蓝牌”
C. 事件“甲分得1张白牌”与事件“乙分得2张白牌”
D. 事件“甲分得2张白牌”与事件“乙分得1张黑牌”
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了纪念“一带一路”倡议提出五周年,某城市举办了一场知识竞赛,为了了解市民对“一带一路”知识的掌握情况,从回收的有效答卷中按青年组和老年组各随机抽取了40份答卷,发现成绩都在
内,现将成绩按区间
,
,
,
，
进行分组,绘制成如下的频率分布直方图．
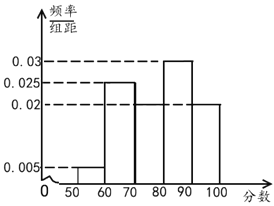
青年组
中老年组
(1)利用直方图估计青年组的中位数和老年组的平均数；
(2)从青年组,的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自分数段的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图1，已知菱形
的对角线
交于点
，点
为线段
的中点，
，
，将三角形
沿线段
折起到
的位置，
，如图2所示．
（Ⅰ）证明：平面
平面
；
（Ⅱ）求三棱锥
的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在三棱锥
中，N为CD的中点，M是AC上一点.
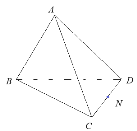
（1）若M为AC的中点，求证：AD//平面BMN；
（2）若
，平面
平面BCD,
，求直线AC与平面BMN所成的角的余弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
