
分析 (I)格局等差数列的通项公式列方程组解出公差,得出通项公式,代入求和公式计算Sn;
(II)根据等比数列的通项公式列方程组解出首项和公比即可得出通项公式.
解答 解:(I)设{an}的公差为d,则a2=2+d,a3=2+2d,
∴(2+d)(2+2d)=40,解得:d=3或d=-6.
∵{an}为递减数列,∴d=-6.
∴an=2-6(n-1)=8-6n,
Sn=$\frac{{a}_{1}+{a}_{n}}{2}$•n=-3n2+5n.
(II)由(I)可知a2=-4,a4=-16.
设等比数列{bn}的公比为q,
则$\left\{\begin{array}{l}{{b}_{1}q=-4}\\{{b}_{1}{q}^{3}=-16}\end{array}\right.$,解得$\left\{\begin{array}{l}{{b}_{1}=-2}\\{q=2}\end{array}\right.$或$\left\{\begin{array}{l}{{b}_{1}=2}\\{q=-2}\end{array}\right.$.
∵{bn}为递减数列,∴$\left\{\begin{array}{l}{{b}_{1}=-2}\\{q=2}\end{array}\right.$.
∴bn=-2•2n-1=-2n.
点评 本题考查了等差数列,等比数列的通项公式,求和公式,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{9}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | -$\frac{5}{3}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在海滨某城市附近海面有一台风,据监测,台风中心位于城市A的南偏东15°方向、距城市120$\sqrt{3}$km的海面P处,并以20km/h的速度向北偏西45°方向移动,如果台风侵袭的范围为圆型区域,半径为120km,几小时后该城市开始受到台风的侵袭?
如图,在海滨某城市附近海面有一台风,据监测,台风中心位于城市A的南偏东15°方向、距城市120$\sqrt{3}$km的海面P处,并以20km/h的速度向北偏西45°方向移动,如果台风侵袭的范围为圆型区域,半径为120km,几小时后该城市开始受到台风的侵袭?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 8$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
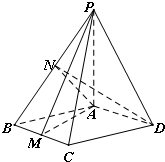 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=$\sqrt{6}$,四边形ABCD是边长为2的菱形,∠ABC=60°,M,N分别为BC和PB的中点..
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=$\sqrt{6}$,四边形ABCD是边长为2的菱形,∠ABC=60°,M,N分别为BC和PB的中点..查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com