Question

7．在三棱锥S-ABC中，AB⊥BC，AB=BC=$\sqrt{2}$，SA=SC=2．AC的中点为M，∠SMB的余弦值为$\frac{\sqrt{3}}{3}$，若S、A、B、C都在同一球面上，则该球的表面积为（　　）

• A． $\frac{3π}{2}$
• B． 2π
• C． 6π
• D． $\sqrt{6}$π

Answer 1

分析 根据定义，先作出它的平面角，如图所示．进一步分析此三棱锥的结构特征，找出其外接球半径的几何或数量表示，再进行计算．

解答 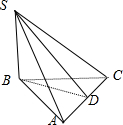解：如图所示：
取AC中点D，连接SD，BD，则由AB=BC，SA=SC得出SD⊥AC，BD⊥AC，
∴∠SDB为S-AC-B的平面角，且AC⊥面SBD．
由题意：AB⊥BC，AB=BC=$\sqrt{2}$，得：△ABC为等腰直角三角形，且AC=2，
又∵BD⊥AC，故BD=AD=$\frac{1}{2}$AC，
在△SBD中，BD=$\frac{1}{2}×2$=1，
在△SAC中，SD²=SA²-AD²=2²-1²=3，
在△SBD中，由余弦定理得SB²=SD²+BD²-2SD•BDcos∠SDB=3+1-2×$\sqrt{3}×1×\frac{\sqrt{3}}{3}$=2，
满足SB²=SD²-BD²，∴∠SBD=90°，SB⊥BD，
又SB⊥AC，BD∩AC=D，∴SB⊥面ABC．
以SB，BA，BC为顶点可以补成一个棱长为2的正方体，S、A、B、C都在正方体的外接球上，
正方体的对角线为球的一条直径，∴2R=$\sqrt{3}×\sqrt{2}$，R=$\frac{\sqrt{6}}{2}$，球的表面积S=4$π×\frac{6}{4}$=6π．
故选：C．

点评 本题考查面面角，考查球的表面积，解题的关键是确定外接圆的半径，属于中档题．