
【题目】已知集合A={x|1≤x≤5},B={x|log2x>1}
(1)分别求A∩B,(RB)∪A;
(2)已知集合C={x|2a﹣1≤x≤a+1},若CA,求实数a的取值范围.
【答案】
(1)解:由题意:集合A={x|1≤x≤5},B={x|log2x>1}={x|x>2},
RB={x|x≤2},
那么:A∩B={x|2<x≤5};
(CRB)∪A={x|x≤2}∪{x|1≤x≤5}={x|x≤5}
(2)解:集合C={x|2a﹣1≤x≤a+1},
∵CA,
∴①当C=时,满足题意,此时2a﹣1>a+1,解得:a>2.
②当C≠时,要使CA,需满足:  ,
,
解得:1≤a≤2.
综合①②,可得a的取值范围是[1,+∞)
【解析】(1)根据集合的基本运算即可求A∩B,(UB)∪A;(2)根据CA,建立条件关系即可求实数a的取值范围.
【考点精析】关于本题考查的交、并、补集的混合运算,需要了解求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】过△ABC所在平面α外一点P,作PO⊥α,垂足为O,连接PA,PB,PC,若点O是△ABC的内心,则( )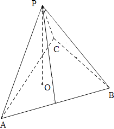
A.PA=PB=PC
B.点P到AB,BC,AC的距离相等
C.PA⊥PB,PB⊥PC,PC⊥PA
D.PA,PB,PC与平面α所成的角相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一汽车厂生产![]() 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
轿车 | 轿车 | 轿车 | |
舒适型 | 100 | 150 |
|
标准型 | 300 | 450 | 600 |
按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有![]() 类轿车10辆.
类轿车10辆.
(I)求![]() 的值;
的值;
(II)用分层抽样的方法在![]() 类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(III)用随机抽样的方法从![]() 类舒适型轿车中抽取8辆,经检测它们的得分
类舒适型轿车中抽取8辆,经检测它们的得分![]() 的值如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数
的值如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数![]() ,设样本平均数为
,设样本平均数为![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年春节期间,某服装超市举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.
方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸出2个红球则打6折,若摸出1个红球,则打7折;若没摸出红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利用简单随机抽样从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.在这些用户中,用电量落在区间[150,250]内的户数为( ) 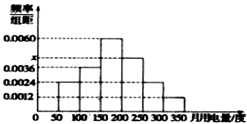
A.46
B.48
C.50
D.52
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:参数方程与极坐标系
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() 为倾斜角),以坐标原点O为极点,
为倾斜角),以坐标原点O为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线![]() 的直角坐标方程,并 求C的焦点F的直角坐标;
的直角坐标方程,并 求C的焦点F的直角坐标;
(2)已知点![]() ,若直线
,若直线![]() 与C相交于A,B两点,且
与C相交于A,B两点,且![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com