
| A. | ①③ | B. | ②③④ | C. | ③④ | D. | ②④ |
分析 由题意先化简解析式,在同一坐标系中画出y=sinx和y=cosx的图象,由图象和正弦、余弦函数的性质,分别判断四个命题的真假.
解答 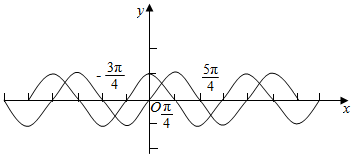 解:由题意得,f(x)=$\left\{\begin{array}{l}{sinx,sinx≥cosx}\\{cosx,sinx<cosx}\end{array}\right.$
解:由题意得,f(x)=$\left\{\begin{array}{l}{sinx,sinx≥cosx}\\{cosx,sinx<cosx}\end{array}\right.$
=$\left\{\begin{array}{l}{sinx,x∈[\frac{π}{4}+2kπ,\frac{5π}{4}+2kπ]}\\{cosx,x∈(-\frac{3π}{4}+2kπ,\frac{π}{4}+2kπ)}\end{array}\right.$
(k∈Z),
在同一坐标系中画出y=sinx和y=cosx的图象:
①、f(x+π)=$\left\{\begin{array}{l}{-sinx,sinx≥cosx}\\{-cosx,sinx<cosx}\end{array}\right.$≠f(x),由图象知函数f(x)的最小正周期为2π,①不正确;
②、由f(x)=$\left\{\begin{array}{l}{sinx,x∈[\frac{π}{4}+2kπ,\frac{5π}{4}+2kπ]}\\{cosx,x∈(-\frac{3π}{4}+2kπ,\frac{π}{4}+2kπ)}\end{array}\right.$得(k∈Z),
f(x)的值域是$[-\frac{\sqrt{2}}{2},1]$,②不正确;
③、由正弦和余弦函数的单调性知,
f(x)的递增区间为[2kπ+$\frac{π}{4}$,2kπ+$\frac{π}{2}$],[2kπ+$\frac{5π}{4}$,2kπ+2π](k∈Z),③正确;
④、由正弦和余弦函数的图象可得,f(x)关于直线x=$\frac{π}{4}$+kπ,k∈Z对称,④正确,
综上可得,③④,
故选:C.
点评 本题考查正弦、余弦函数的图象以及性质,由图象和三角函数的性质判断命题的真假.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
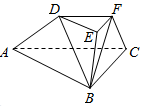 如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.
如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
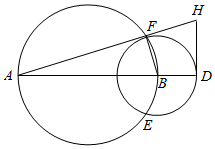 如图,A,B,D三点共线,以AB为直径的圆与以BD为半径的圆交于E,F,DH切圆B于点D,DH交AF于H.
如图,A,B,D三点共线,以AB为直径的圆与以BD为半径的圆交于E,F,DH切圆B于点D,DH交AF于H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com