
【题目】某校从高二年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
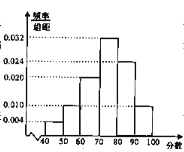
(1)若该校高二年级共有学生1000人,试估计成绩不低于60分的人数;
(2)求该校高二年级全体学生期中考试成绩的众数、中位数和平均数的估计值.
【答案】(1)860(2)75,75,74.2
【解析】
试题分析:(1)根据频率分布直方图可求得成绩不低于60分的概率值,结合样本容量可求得相应的人数;(2)众数为出现的次数最多的数,中位数为由小到大排列后的位于中间的数,平均数为各组的频率与该组的频数成绩之和
试题解析:(1)成绩不低于60分所占的频率为:1-(0.004+0.010)*10=0.86
所以成绩不低于60分的人数估计值为:1000*0.86=860(人) -----------4分
(2)众数估计值:75 ------------6分
设中位数为x,则(x-70)*0.032=0.5-0.04-0.1-0.2,解得x=75 ---------9分
平均数估计值:![]() s----12分
s----12分


科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线的方程;
处的切线的方程;
(Ⅱ)如果存在![]() ,使得
,使得![]() 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数![]() ;
;
(Ⅲ)如果对任意的![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,椭圆上的点
,椭圆上的点![]() 满足
满足![]() ,且
,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,过点
,过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,证明:点
,证明:点![]() 总在直线
总在直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图:
分组的频率分布直方图如图:
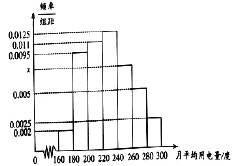
(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)求月平均用电量的众数和中位数;
(Ⅲ)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在
的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】口袋中装有质地大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸一个球,记下编号,放回后乙再摸一个球,记下编号.如果两个编号的和为偶数就算甲胜,否则算乙胜.
(1)求甲胜且编号的和为6的事件发生的概率;
(2)这种游戏规则公平吗?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地参加2015 年夏令营的![]() 名学生的身体健康情况,将学生编号为
名学生的身体健康情况,将学生编号为![]() ,采用系统抽样的方法抽取一个容量为
,采用系统抽样的方法抽取一个容量为![]() 的样本,且抽到的最小号码为
的样本,且抽到的最小号码为![]() ,已知这
,已知这![]() 名学生分住在三个营区,从
名学生分住在三个营区,从![]() 到
到![]() 在第一营区,从
在第一营区,从![]() 到
到![]() 在第二营区,从
在第二营区,从![]() 到
到![]() 在第三营区,则第一、第二、第三营区被抽中的人数分别为( )
在第三营区,则第一、第二、第三营区被抽中的人数分别为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列{bn}中的b3、b4、b5.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)数列{bn}的前n项和为Sn,求证:数列{Sn+![]() }是等比数列.
}是等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为方便市民休闲观光,市政府计划在半径为200米,圆心角为![]() 的扇形广场内(如图所示),沿
的扇形广场内(如图所示),沿![]() 边界修建观光道路,其中
边界修建观光道路,其中![]() 分别在线段
分别在线段![]() 上,且
上,且![]() 两点间距离为定长
两点间距离为定长![]() 米.
米.
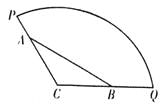
(1)当![]() 时,求观光道
时,求观光道![]() 段的长度;
段的长度;
(2)为提高观光效果,应尽量增加观光道路总长度,试确定图中![]() 两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com