
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,椭圆上的点
,椭圆上的点![]() 满足
满足![]() ,且
,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,过点
,过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,证明:点
,证明:点![]() 总在直线
总在直线![]() 上.
上.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】某校高三年级在高校自主招生期间,把学生的平时成绩按“百分制”折算并排序,选出前300名学生,并对这300名学生按成绩分组,第一组![]() ,第二组
,第二组![]() ,第三组
,第三组![]() ,第四组
,第四组![]() ,第五组
,第五组![]() ,如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列.
,如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列.
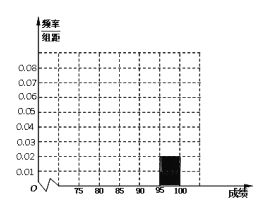
(I)请在图中补全频率直方图;
(II)若![]() 大学决定在成绩高的第4,5组中用分层抽样的方法抽取6名学生,并且分成2组,每组3人进行面试,求95分(包括95分)以上的同学被分在同一个小组的概率.
大学决定在成绩高的第4,5组中用分层抽样的方法抽取6名学生,并且分成2组,每组3人进行面试,求95分(包括95分)以上的同学被分在同一个小组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三数学奥林匹克竞赛集训队的一次数学测试成绩的茎叶图(图1)和频率分布直方图(图2)都受到不同程度的破坏,可见部分如图所示,据此解答如下问题.
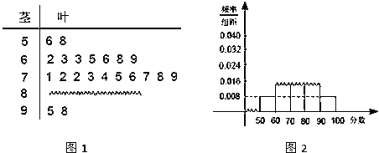
(1)求该集训队总人数及分数在[80,90)之间的频数;
(2)计算频率分布直方图中[80,90)的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生的答题情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高二年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
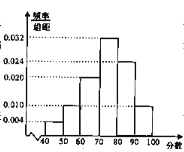
(1)若该校高二年级共有学生1000人,试估计成绩不低于60分的人数;
(2)求该校高二年级全体学生期中考试成绩的众数、中位数和平均数的估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx(a≠0)的导函数f′(x)=-2x+7,数列{an}的前n项和为Sn,点Pn(n,Sn)(n∈N*)均在函数y=f(x)的图象上,求数列{an}的通项公式及Sn的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com