
已知多面体ABCDFE中, 四边形ABCD为矩形,AB∥EF,AF⊥BF,平面ABEF⊥平面ABCD, O、M分别为AB、FC的中点,且AB = 2,AD = EF = 1.
(Ⅰ)求证:AF⊥平面FBC;
(Ⅱ)求证:OM∥平面DAF;
(Ⅲ)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为VF-ABCD,VF-CBE,求VF-ABCD∶VF-CBE 的值.

解:(Ⅰ) 平面ABEF⊥平面ABCD ,平面ABEF
平面ABEF⊥平面ABCD ,平面ABEF 平面ABCD=AB
平面ABCD=AB
BC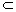 平面ABCD,而四边形ABCD为矩形
平面ABCD,而四边形ABCD为矩形  BC⊥AB ,
BC⊥AB ,
 BC⊥平面ABEF
BC⊥平面ABEF
 AF
AF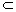 平面ABEF
平面ABEF  BC
BC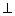 AF
AF  BF
BF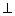 AF,BC
AF,BC BF=B
BF=B
 AF⊥平面FBC
AF⊥平面FBC
(Ⅱ)取FD中点N,连接MN、AN,则MN∥CD,且 MN=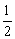 CD,又四边形ABCD为矩形,
CD,又四边形ABCD为矩形,
 MN∥OA,且MN=OA
MN∥OA,且MN=OA  四边形AOMN为平行四边形,
四边形AOMN为平行四边形, OM∥ON
OM∥ON
又 OM
OM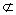 平面DAF,ON
平面DAF,ON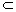 平面DAF
平面DAF  OM∥平面DAF
OM∥平面DAF
(Ⅲ)过F作FG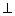 AB与G ,由题意可得:FG
AB与G ,由题意可得:FG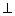 平面ABCD
平面ABCD
 VF-ABCD =
VF-ABCD =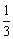 S矩形ABCDE·FG =
S矩形ABCDE·FG = 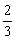 FG
FG
 CF
CF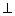 平面ABEF
平面ABEF  VF-CBE = VC-BFE =
VF-CBE = VC-BFE =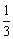 S△BFE·CB =
S△BFE·CB = 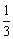
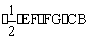 =
= 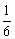 FG
FG
 VF-ABCD∶VF-CBE = 4∶1
VF-ABCD∶VF-CBE = 4∶1


科目:高中数学 来源: 题型:
已知0< <b,且f (x)=
<b,且f (x)=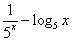 ,则下列大小关系式成立的是( ).
,则下列大小关系式成立的是( ).
A、 f (b)< f (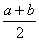 )<f (
)<f (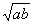 ) B、f (
) B、f (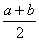 )<f (b)< f (
)<f (b)< f (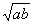 )
)
C、f (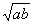 )< f (
)< f (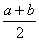 )<f (
)<f ( ) D、 f (
) D、 f ( )< f (
)< f (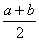 )<f (
)<f (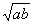 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=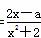 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.
(1) 求实数a的值组成的集合A;
(2) 设x1、x2是关于x的方程f(x)=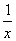 的两个相异实根,若对任意a∈A及t∈[-1,1],不等式m2+tm+1≥|x1-x2|恒成立,求实数m的取值范围.
的两个相异实根,若对任意a∈A及t∈[-1,1],不等式m2+tm+1≥|x1-x2|恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com